Introduction to Maxwell’s equations
How Maxwell’s equations are defined for electrostatics and magnetostatics? This article aims to get better understanding of static properties of magnetic and electric field to get better understanding of faraday’s law of Electromagnetic induction and how it will have related to the curl of electrical field. To get better understanding, the use of Maxwell equations. The equations which describes the relationship between as change in magnetic field and change in electric field are called the Maxwell’s equations. Maxwell equations are extension of the famous works of Gauss for the electric and magnetic field, faradays and lastly Ampere. Maxwell equations can be written in integral form and as differential form. The differential form of these equations relates the characteristic of vector fields at any given point to the other point and to source densities at given point. Integral form of these equations controls the dependence of a particular field and the amount of source (charge and current) corresponding to the regions in space, large sections and volumes. Mainly these four Maxwell equations provide the strong mathematical background for study of electromagnetic waves which further used in transmission line and antenna’s.
In 19th century, the physicist James Clerk Maxwell explain the electromagnetic phenomenon by using four set of equations. These four equations together with the Lorentz force law explain the major law of magnetism and electricity.
Applications of Maxwell’s Equations
- The first equation is known as Gauss law for electricity (electric field diverge from electric charge).
- The second equation is known as Gauss law for magnetism (no isolated monopoles exist).
- The third one is faraday law of induction (electrical field produce by changing in magnetic field).
- The fourth equations is Ampere’s law with some symmetrical formation that adds another source (changing electric field) for
- Although light was only a wave before Maxwell predictions and mathematical forms, later he confirmed that light is electromagnetic waves that was confirmed by
History of Maxwell’s Equations
- Maxwell’s equations explain classical magnetism and electrodynamics. Like newton’s equation of motion describe classical mechanics. He produced mathematical description of electromagnetic waves and understanding of light
- Maxwell wrote a paper in 1864,”A dynamical theory of electromagnetic field”, in which he explains the theoretical approach of electromagnetism.”
According to paper, equations expressed:
- Relationship between total current, electric displacement and true
- Relation between the induction coefficient of circuit and magnetic lines of
The basis of “action-at-a “electromagnetism, development-opened by André-Marie Ampère, Franz Neumann, Augustin Coulomb, Wilhelm Weber, Gustave Kirchhoff, his successor physical, local communication in between the amount of field; setting a case value field inscape and time, and moment the charge corresponds to the field its specific location
Almost two decades after publication of Maxwell, Rudolf hertz and Oliver Heaviside consolidated Maxwell mathematical equation into four current equations that was written in the form of magnetic and electric field.
The revolutionary nature of these equations was recognized by Einstein who wrote: The mathematical form of these equations and formulation is the most important event in physics since newton’s time, because they form a sort of pattern for new type of law. Richard Feynman a physicist said:” From a long view of history of mankind, there can be a little doubt on that most significant event of 19th century will be judged as discovery of Maxwell laws of electrodynamics”
What are the Maxwell’s Equations?
Maxwell four equations explain the magnetic and electric field arising from distributions of current and electric charges and how these fields will change in time.

OPERATORS:
Where;
∇. Divergence operator
∇ x curl operator
B magnetic field intensity E electric field intensity
D electric displacement field H magnetic field intensity
J free current density
Ρ free charge density

CONTRIBUTION OF MAXWELL IN ELECTROMAGNETICS:
Some 150 years ago, James Clerk Maxwell, an English scientist, developed the scientific concept of electromagnetism. Be aware that electric fields and magnetic fields can combine to form electric waves. An electric field (such as a static that forms when you rub your feet on a carpet), or a magnetic field (such as the one with a magnet in your refrigerator) will not go away on its own. However, Maxwell found that a changing in magnetic field would create a changing in electric field and vice versa.
USE OF MAXWELL EQUATION:
- Equations provide a mathematical model for electrical, optical, and radio technology, such as power generation, wireless communication, electric motors, radar, lenses etc.
- They describe how magnetic fields are generated by charges, currents and changes of
DIFFERENTIAL FORM:
Differential form
It is independent of coordinates and it is an approach to multivariable calculus.
INTEGRAL FORM:
Some numeric value equal to area under the graph over some interval of given function which is definite integral or a new function derivative of which original function (indefinite integral).
MAXWELL EQUATION :01
GAUSS LAW FOR ELECTRIC FIELD:
The first equation is Gauss’s law, named after German polymath Friedrich Gauss (1777–1855), who first wrote it. In 1867 German physicist Wilhelm Weber (1804–1891) wrote article on Gauss’s law.
- Maxwell first equation based on gauss law for electric field, where gauss developed relation between static electric charges and their effect on static
STATEMENT:
“The total flux of the closed surface is equal to the total charge enclosed by the surface.”
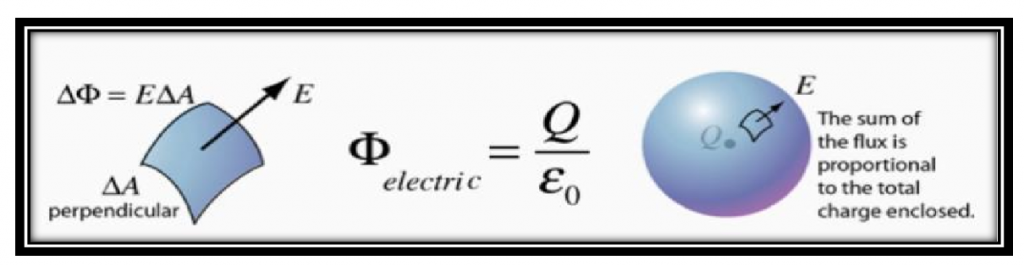
Importance:
- Gauss’s law is very useful in calculating the electric field in case of problems where it is possible to build a closed Such a surface is called the territory of Gaussian.
- Gauss’s law is true in any closed environment, regardless of its nature or
- Symmetric consideration in many cases makes the application of Gauss’s law much easier
Differential form:
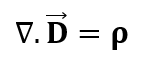
Where D is electric displacement field, ρ is free charge density. It is state that the electric flux through a closed surface area is equal to total charge enclosed in that surface
Integral form:
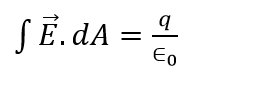
Q is charge enclosed; E is electric field intensity. This integral equation states that the electric flux through closed surface is equal to the net charge enclosed in the surface.
Application:
Electric Field Intensity because of Spherical Surface
Consider the sphere of some length L and radius r centered on the charges. A long line of stationary charge placed as shown in figure
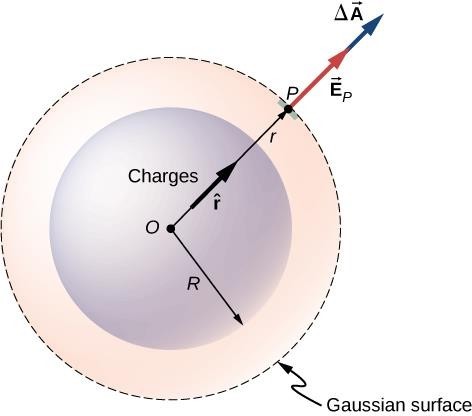
There are the symmetrical, not symmetric and symmetric spherical surfaces as shown in figure:
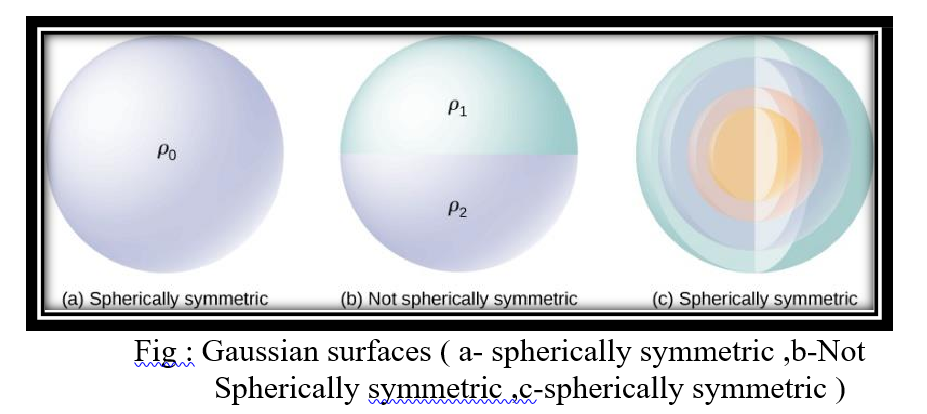

PROBLEM STATEMENT:
A charge of 4×10-8 C is distributed uniformly on the surface of a sphere of radius 1 cm. It is covered by a concentric, hollow conducting sphere of radius 5 cm.
- Find the electric field at a point 2 cm away from the center
- A charge of 6 × 10-8C is placed on the hollow Find the surface charge density on the outer surface of the hollow sphere.
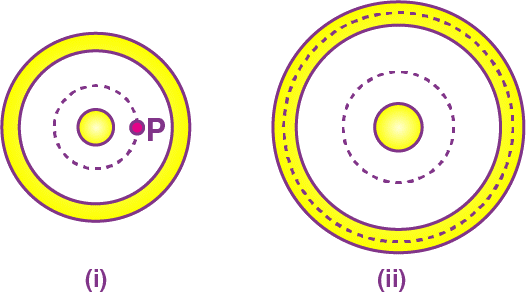
- Let us consider the figure (i).
Suppose, we have to find the field at point P. Draw a concentric spherical surface through P. All the points on this surface are equivalent and by symmetry, the field at all these points will be equal in magnitude and radial in direction.
The flux through this surface = ∮E.dS = ∮EdS=E∮dS = 4π x^2 E. where x = 2 cm = 2 × 10-2 m.
From Gauss law, this flux is equal to the charge q contained inside the surface divided by ε0. Thus,
⇒ 4π x2 E = q/ε0 or, E = q/4πε0x2
= ( 9 × 109) × [(4 × 10-8)/(4 × 10-4)]
= 9 × 105 NC-1.
b)Let us consider the figure (ii).
Take the Gaussian surface through the material of the hollow sphere. As the electric field in a conducting material is zero, the flux ∮E. dS through this Gaussian surface is zero. Using Gauss law, the total charge enclosed must be zero.
Hence, the charge on the inner surface of the hollow sphere is 4 × 10-8C. But the total charge given to this hollow sphere is 6 × C. Hence, the charge on the outer surface will be 10 ×10^-8 C.
MAXWELL EQUATION :02
Gauss Law for Magnetism:
The presence of magnetic field (i.e., monopoles) which can act as sources and sink magnetic field founded by British physicist Paul Dirac (1902-1984) 1931 to describe the electric charges, acquired by American Nobel philosopher to Robert Millikan (1868–1953). monopoles feature prominently in modern gauge-symmetric theories, but they have not been yet observed in our universe.
Statement:
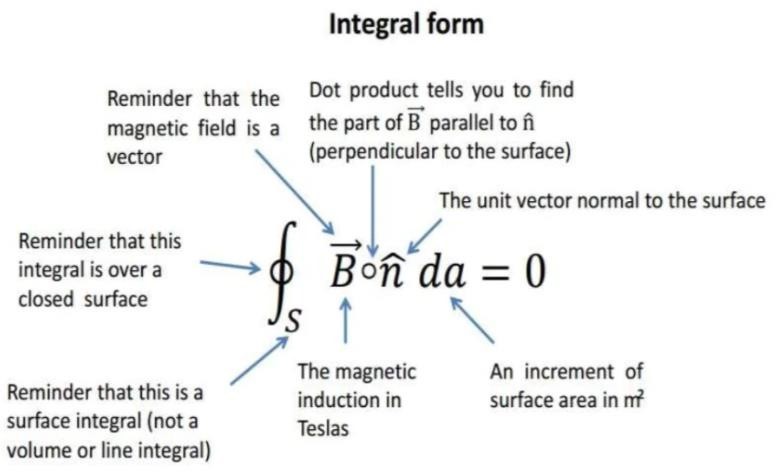
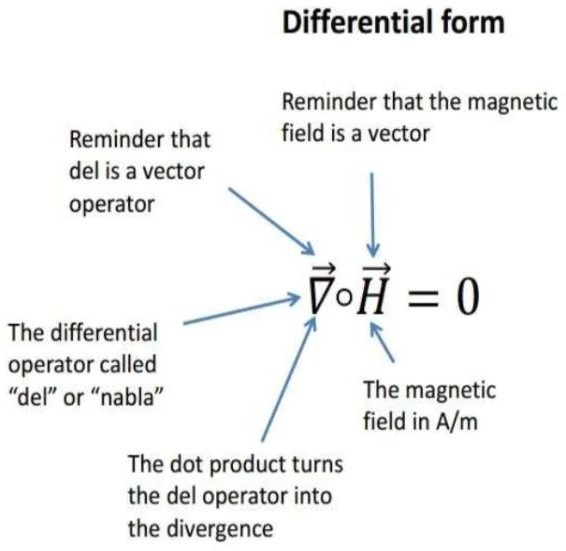
The total magnetic flux passing through a closed surface is zero. the magnetic flux lines are closed in nature, they are originated from north and ending at south. Due to which a closed surface in presence of these lines will have same number of coming and outgoing flux line.
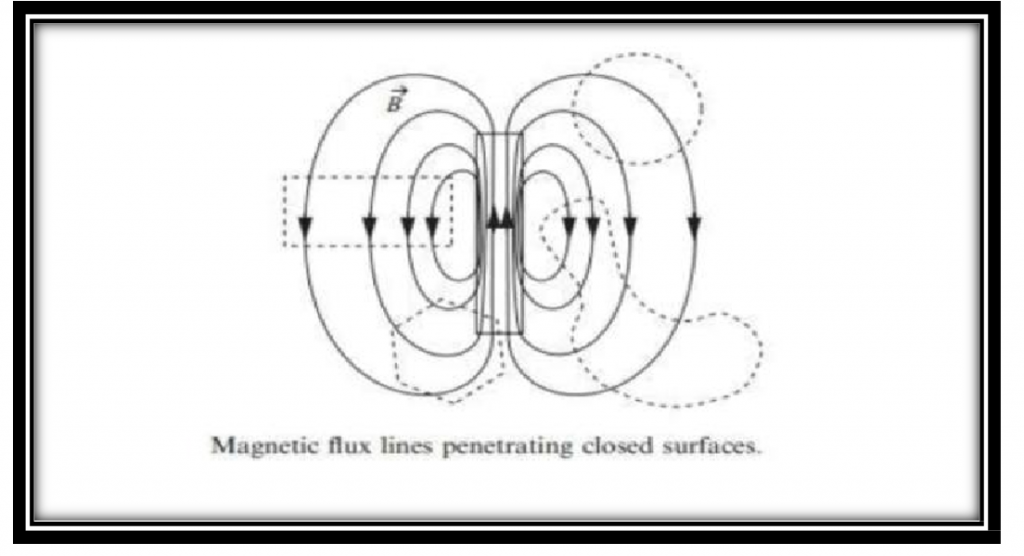
In figure we consider a closed pass in magnetic flux line, you can clearly scene that number of line passing is equal to number of line leaving the surface.
Importance:
Essentially it is stating the impossibility of creating a magnetic monopole; the total magnetic flux through a closed surface is zero.
Integral form:
Differential form:
Divergence of magnetic field lines of unit area should be zero.
Application of Gauss’s Law
Gauss’s law of magnetism also allows you to track field lines. Think of Gaussian surface, such as the “half donut” or “half bagel”, which follows the lines of the “up and up and up” field from the
magnetic spine (like the earth’s axis) to the equator, and then “cut backwards inwards” until they meet and its original field storage:

As we know: ∫B.dA=0, in this case the surface integral is zero along the field lines. But positive along the outside of sphere at bottom. Negative the rest of the way “in” inside the sphere
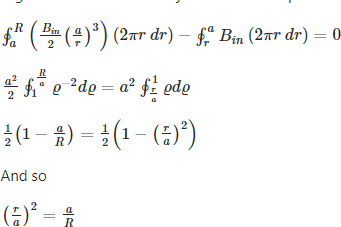
Thus, we know that a field line “downwards” through the equatorial plane at radius R originated from
radius.
PROBLEM STATEMENT:
Why the magnetic flux through a closed surface be equals to zero ?
Answer:
Gauss’ Law for magnetism applies to the magnetic flux through a closed surface. Here the area vector points out from the surface. Because magnetic field lines are continuous loops, all closed surfaces have as many magnetic field lines going in as coming out. Hence, the net magnetic flux through a closed surface is zero.
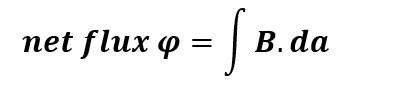
Maxwell’s 3rd Equation
Faradays Law OF Magnetic Induction
Faradays discovered his equation of electromagnetic induction in 1831. But unable to mathematically describe the process. He used the geometric concept of magnetic line of force by Rene Descartes and tells the existence of electronic state.
Statement:
It is stated that, the time varying or changing magnetic field will always produce an electric field
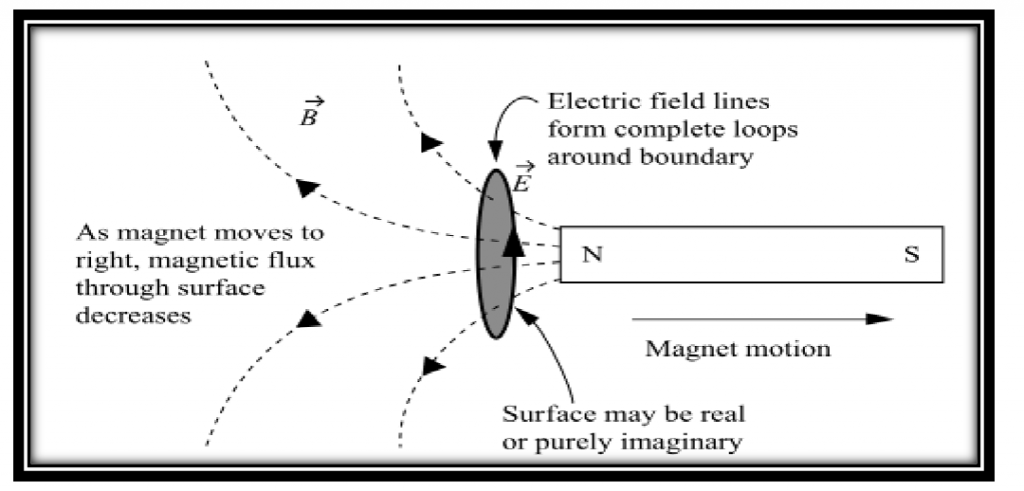
Maxwell third equation is advanced form of faraday law of induction, it is state that when a conducting wire with n number of turns is placed in time varying magnetic field, an emf is induced in that conducting wire. This is given by lenze law that induced emf will always oppose the cause which produces it.
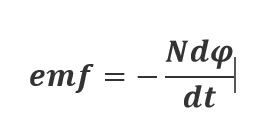
Importance:
Maxwell third equation tells you how change in magnetic field will produce electric field. It is basic of electric generators, the third equation is used in phenomenon of generation of electricity by generators.
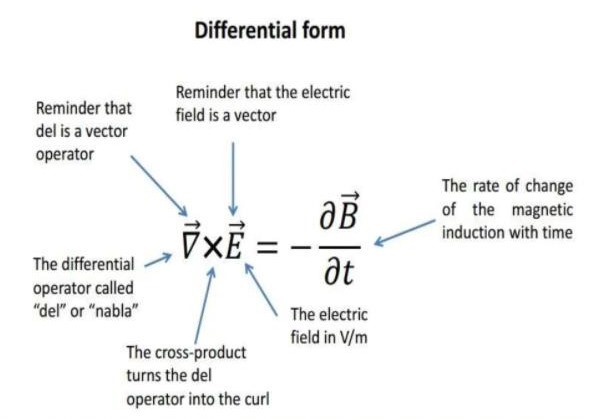
Differential form:
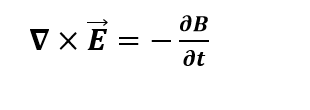
This is differential form of third equation of Maxwell. On the left side of equation, it is curl of electric field, it will tell about the tendency of electric field of lines to circulate about a point. So the right side of the equation, show about rate of change of magnetic field.
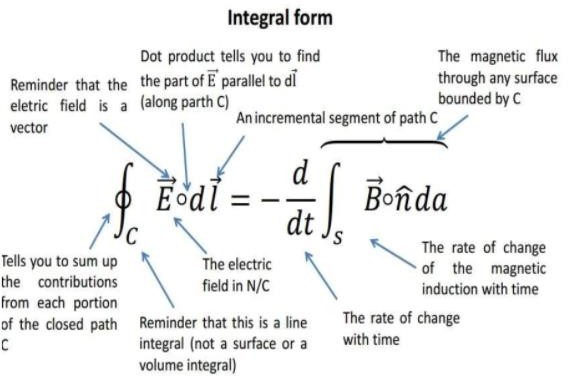
Integral form:
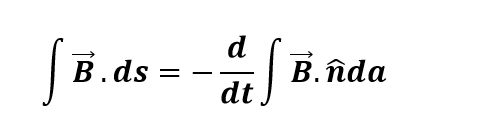
Equation says, if flux through any surface changing will produce an electric field around that surface. If any conducting material present at boundary of surface then emf will induced in it that further produce a current in that surface.
“Change in magnetic field through a surface will produce a induced emf around that surface.”
Application:
Following are some applications:
- It is used for electricity generation.
- It is used in magnetic tape.
- This phenomenon is used in MRI
PROBLEM STATEMENT:
A loop of area 200c is positioned perpendicular to a uniform magnetic field. Without changing in direction of the magnetic field, its magnitude is reduced by 0.08T in the time interval 0.02s. Find the average induced emf in the loop?
Solution:
According to Faraday’s law of induction equation, a changing magnetic flux through a closed surface bounded by a wire, creates an emf with a magnitude of
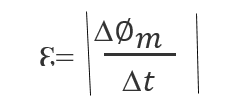
B⋅A where is a unit vector (a vector whose its magnitude is unity) normal (perpendicular) to that surface.
Also read here: