What are the sequences?

What are the sequences and arithmetic progressions? Sequences are also called the progressions. If the numbers are generated according to a certain rule such that each consecutive number has a specific relation with its neighbors then they are said to form a sequence. You can consider sequences as list of ordered pairs. Sequences are represented by {a_n} where n is an integer. The value of n can be any integer or from natural number (1,2,3,….) which is called the domain of sequence. Each number in the sequence is called term.

So, if we are having an expression for a sequence, we can generate its terms by substituting different values of n. Consider the following sequence.

\begin{equation}
b_{n}=2+(-1)^{n}
\end{equation}

Starting n form 1 we can generate the sequence like

b₁=2+(-1)¹=1

b₂=2+(-1)²=3

b₃=2+(-1)³=1

b₄=2+(-1)⁴=3 and so on. So in sequence form it is written as: 1,3,1,3,…….

What are the finite and infinite sequences?

If the last or final term of the sequence is known then they are called the finite sequences and if the last term of sequence is not known then they are called infinite sequences.

Examples

finite sequence: {1,2,3,…..10}

infinite sequence: {5,10,15,20,……}

What is the Arithmetic Progression?

Arithmetic progression is the type of the sequences, where two consecutive numbers have same common difference. For example if you look at the following sequence you can see that the common difference is same for any two consecutive terms.

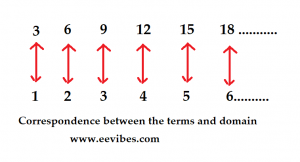
3,6,9,12,15,……

here 6-3=9-6=12-9=15-12=3. So, the common difference is 3

If you the correspondence established between the sequence terms then it will look like

How to generate the nth term of the Arithmetic Progression (AP)?

As we know that for the arithmetic progression, common difference is same. So for generating the nth term of sequence, we will use this concept.

a₂-a₁=d       à a₂= a₁+d

a₃-a₂=d       à a₃= a₂+d       ——–(i) Substitute the value of  a₂ from above equation.

à a₃= (a₁+d )+d= a₁+2d

Similarly

a₃= a₁+2d

a_n= a₁+(n-1)d

This is the expression of nth general term of a sequence. Which means if we have the first term of A.P and the difference d, we can find any other term of the AP.

Selective problems solution of chapter no. 6 F.Sc Part 1

If the 5th term of an AP is 16 and the 20th term is 46, what is the 12th term?

Solution:

Since

Since a₅=16 = a₁+4d

Also

A₂₀=46 = a₁+19d

So

a₁+4d=16

a₁+19d=46

Solving them simultaneously, we will get

15d=30 à d=2

So,

a₁+4(2)=16

a₁+8=16

and a₁= 2

Hence,

a₁₂= a₁+11d

=2+11(2)

=24

How many terms are there in AP in which a₁ =11, an=68 and d=3?

Solution

Here we have to find n actually.

a₁ = 11

a_n= a₁+(n-1)d=68

so substitute the value of a₁ and d, we get

68=11+(n-1)(3)

68-11=3(n-1)

57=3(n-1)

19=n-1

n=20

So, 68 is the 20th term of A.P

If 1/a, 1/b, and 1/c are in A.P then show that common difference is (a-c)/2ac

Solution

Since they are in A.P, so common difference should be same

d=1/b-1/a=(a-b)/ab =>d+(1/a)=1/b=>(ad+1)/a=1/b or b=a/(ad+1)

Similarly,

d=1/c-1/b

Substitute the value of b here, you will get

d=1/c- (ad+1)/a

d=a-c(ad+1)/ac

d=(a-acd-c)/ac

acd=a-acd-c

or

acd+acd=a-c

2acd=a-c

or

d=(a-c)/2ac

Hence proved.

What is the arithmetic mean?

Any number A is said to be an arithmetic mean between two numbers a and b if a,A, b are in A.P.

Since a,A,b are in A.P

So,

d=A-a and d=b-A

by comparing both, we get

A-a=b-A

or

A=(a+b)/2

If three consecutive terms are in A.P, then the middle term is actually the arithmetic mean between the extreme terms.

If a_n-1,a_n and a_n+1 are in A.P then, we can write the general term as:

\begin{equation}
a_{n}=\frac{a_{n-1}+a_{n+1}}{2}
\end{equation}

How to find n Arithmetic means between two given numbers?

This is very simple. Lets us consider that there are A₁, A_2, A₃, A₄,……..A_n arithmetic means present between two numbers a and b such that

a, A₁, A_2, A₃, A₄,……..A_n ,b

If they all are in A.P and a₁ = a and a_n+2 = b

then

$$
\begin{gathered}
a_{n+2}=b=a_{1}+(n+2-1) d \\
b=a_{1}+(n+1) d \\
d=\frac{b-a_{1}}{n+1}
\end{gathered}
$$
Here $a_{1}=a$
So

\begin{equation}
d=\frac{b-a}{n+1}
\end{equation}

Hence

A₁=a+\begin{equation}
d=\frac{b-a}{n+1}
\end{equation}

=

$$
\begin{gathered}
A_{1}=\frac{[a(n+1)+b-a]}{n+1} \\
A_{1}=\frac{[(a n+a)+b-a]}{n+1} \\
A_{1}=\frac{a n+a+b-a}{n+1} \\
A_{1}=\frac{a n+b}{n+1}
\end{gathered}
$$
Similarly,
$$
\begin{gathered}
A_{2}=a+2\left(\frac{b-a}{n+1}\right)=\frac{(n-1) a+2 b}{n+1} \\
A_{3}=a+3\left(\frac{b-a}{n+1}\right)=\frac{(n-2) a+3 b}{n+1} \\
A_{n}=a+n\left(\frac{b-a}{n+1}\right)=\frac{(n-(n-1)) a+n b}{n+1} \\
A_{n}=a+n\left(\frac{b-a}{n+1}\right)=\frac{a+n b}{n+1}
\end{gathered}
$$

Show that the sum of n A.Ms between a and b is equal to n times of their A.M

Proof

From the above we have determined the values of n arithmetic means between numbers a and b. They are equal to

\begin{equation}
\begin{gathered}
A_{1}=\frac{a n+b}{n+1} \\
A_{2}=a+2\left(\frac{b-a}{n+1}\right)=\frac{(n-1) a+2 b}{n+1} \\
A_{3}=a+3\left(\frac{b-a}{n+1}\right)=\frac{(n-2) a+3 b}{n+1} \\
A_{n}=a+n\left(\frac{b-a}{n+1}\right)=\frac{(n-(n-1)) a+n b}{n+1} \\
A_{n}=a+n\left(\frac{b-a}{n+1}\right)=\frac{a+n b}{n+1}
\end{gathered}
\end{equation}

Now lets find their sum, that is

A₁ +A₂ +A₃+A₄+A_n

$$
a+\frac{b-a}{n+1}+a+2\left(\frac{b-a}{n+1}\right)+a+3\left(\frac{b-a}{n+1}\right)+\cdots \ldots .++n\left(\frac{b-a}{n+1}\right)
$$
So,
$$
\begin{gathered}
n a+\left(\frac{b-a}{n+1}\right)[1+2+3+\cdots .+n] \\
n a+\left(\frac{b-a}{n+1}\right) \frac{n(n+1)}{2} \\
=n a+\frac{n(b-a)}{2} \\
=\frac{2 a+n b-n a}{2} \\
=\frac{a n+n b}{2} \\
=\frac{n(a+b)}{2}
\end{gathered}
$$

which is the desired result.