
Introduction to Block Matrices
What are the Block Matrices? In matrix multiplication, whenever the order is high and we have some repeated entries in the matrix we prefer to use the concept of block matrices multiplication.
In this approach a submatrix of a matrix A is obtained by deleting certain number of rows and/or columns. It is also called partitioning of matrix and these small portions of the matrix are called the Blocks of A.
Example of Block Matrices
Consider the following matrix A

Here it can be seen how the matrix A is divided into sub-matrices called block and finally A has been written in terms of the Block matrices.
Now if we want to multiply two matrices, we can use the concept of Block matrix multiplication given that the order of multiplication should be satisfied.
Compute AB using block multiplication for the given matrices.
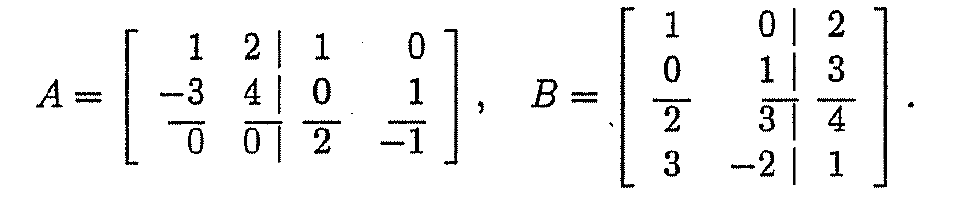
Solution:
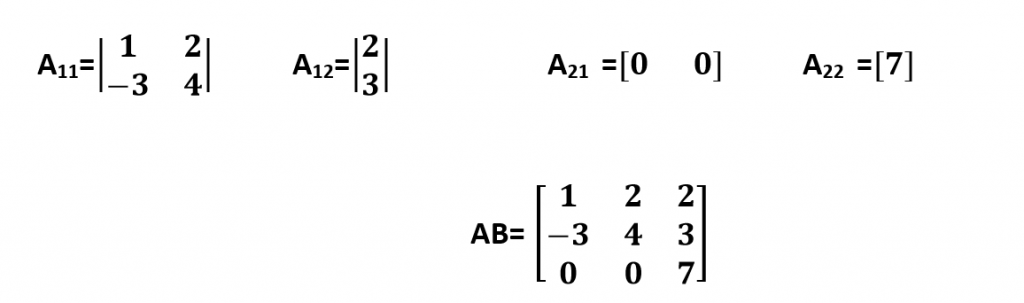
In the above example the resultant matrix is of order 3×3.
This type of multiplication is helpful when we have repeated sequence of Identity matrices.
Also read here
How to test the given vectors are linearly independent or not?