Introduction to significant figures
what are the significant figures? how they are used in numerical analysis? At whatever point we utilize a number in a calculation, we should have confirmation that it can be utilized with certainty. For instance, Fig. below portrays a speedometer and odometer from a vehicle. Visual assessment of the speedometer shows that the vehicle is voyaging somewhere in the range of 48 and 49 km/h. Since the pointer is higher than the midpoint between the markers on the measure, we can say with affirmation that the vehicle is going at roughly 49 km/h. We believe in this outcome since at least two sensible people perusing this measure would come to a similar end result. Notwithstanding, let us state that we demand that the speed be assessed to one decimal spot. For this case, one individual may state 48.8, though another might state 48.9 km/h.
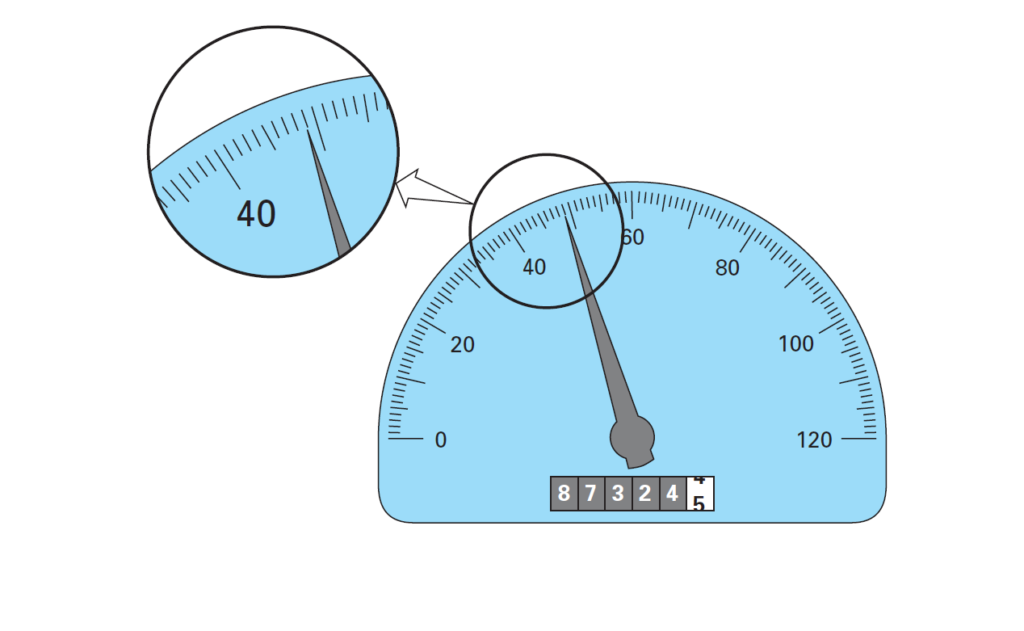
Accordingly, due to the furthest reaches of this instrument, just the initial two digits can be utilized with certainty. Assessments of the third digit (or higher) should be seen as approximations. It is outrageous to guarantee, based on this speedometer, that the vehicle is going at 48.8642138 km/h. Conversely, the odometer gives up to six certain digits. From above Fig., we can reason that the vehicle has voyaged marginally under 87,324.5 km during its lifetime. For this situation, the seventh digit (and higher) is questionable. The idea of a huge figure, or digit, has been created to officially assign the dependability of a mathematical worth. The critical digits of a number are those that can be utilized with certainty.
They compare to the quantity of specific digits in addition to one assessed digit. For instance, the speedometer and the odometer in Fig. 3.1 yield readings of three also, seven huge figures, individually. For the speedometer, the two certain digits are 48. It is ordinary to set the assessed digit at one-portion of the littlest scale division on the estimation gadget. In this manner the speedometer perusing would comprise of the three huge figures: 48.5. Likewise, the odometer would yield a seven-huge figure perusing of 87,324.45. In spite of the fact that it is normally a direct method to determine the huge figures of a number, a few cases can prompt disarray. For instance, zeros are not generally huge figures since they might be essential just to find a decimal point. The numbers 0.00001845, 0.0001845, and 0.001845 all have four critical figures. Additionally, when following zeros are utilized in enormous numbers, it isn’t clear the number of, assuming any, of the zeros are critical.
For instance, at face esteem the number 45,300 may have three, four, or five critical digits, contingent upon whether the zeros are known with certainty. Such vulnerability can be settled by utilizing logical documentation, where 4.53 × 104, 4.530 × 104, 4.5300 × 104 assign that the number is known to three, four, and five critical figures, separately. The idea of critical figures has two significant ramifications for our investigation of mathematical techniques:
1. As presented in the falling parachutist issue, mathematical techniques yield inexact results. We should, in this way, create models to indicate how certain we are in our rough outcome. One approach to do this is as far as huge figures. For instance, we may conclude that our estimation is satisfactory on the off chance that it is right to four critical figures.
2. Despite the fact that amounts, for example, π, e, or
√7 speak to explicit amounts, they can’t be communicated precisely by a predetermined number of digits. For instance, π = 3.141592653589793238462643. . . ceaselessly. Since PCs hold just a limited number of critical figures, such numbers can never be spoken to precisely. The oversight of the excess huge figures is canceled round mistake. Both adjust blunder and the utilization of critical figures to communicate our trust in a mathematical outcome will be investigated in detail in ensuing segments. Moreover, the idea of huge figures will have significance to our meaning of exactness and accuracy in the next area.
What is the meaning of accuracy and precision?
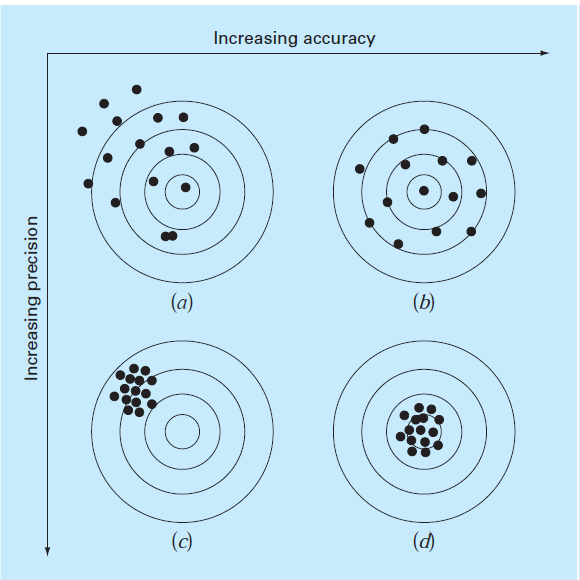
The blunders related with the two counts and estimations can be portrayed with respect to their exactness and accuracy. Precision alludes to how intently a processed or estimated esteem concurs with the genuine worth. Exactness alludes to how intently individual registered or then again estimated values concur with one another. These ideas can be represented graphically utilizing a relationship from target practice. The slug openings on each focus in Fig. below can be considered as the forecasts of a mathematical procedure, while the bull’s-eye speaks to reality. Mistake (additionally called inclination) is characterized as deliberate deviation from reality.
Accordingly, in spite of the fact that the shots in below Fig.( c) are more firmly gathered than those in below Fig. (a), the two cases are similarly one-sided in light of the fact that they are both focused on the upper left quadrant of the objective. Imprecision (additionally called vulnerability), then again, alludes to the size of the disperse. In this manner, in spite of the fact that Fig. (b) and d are similarly precise (that is, focused on the bull’s-eye), the last is more exact in light of the fact that the shots are firmly gathered. Mathematical strategies ought to be adequately exact or impartial to meet the prerequisites of a specific designing issue. They additionally ought to be exact enough for sufficient designing plan.
Also read here:
https://eevibes.com/what-is-the-meaning-of-interpolation-what-are-the-types-of-interpolation/