Gram Schmidt Procedure
The Gram Schmidt procedure is used for orthogonalizing or orthonormalizing the given set of Vectors. If we are given the set of vectors
\begin{equation}
V_{1}, V_{2}, V_{3}, \ldots \ldots, V_{n}
\end{equation}
We can orthogonalize them if they are linearly independent. If the given set of vector does not consist of linearly independent vectors then we can not orthogonalize them using Gram Schmidt Procedure.
Procedure
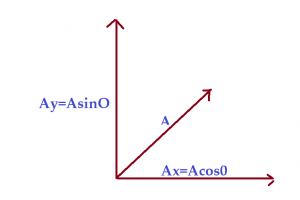
This method uses the idea of components of a vector and then finding the projection of a vector. Since we all know that a vector can be represented as a summation of its components. So, if A is a vector in 2D then it can be written as
$$
\vec{A}=A_{x}+A_{y}
$$
Where
$$
\begin{aligned}
&A_{x}=A \cos \theta \\
&A_{y}=A \operatorname{Sin} \theta
\end{aligned}
$$
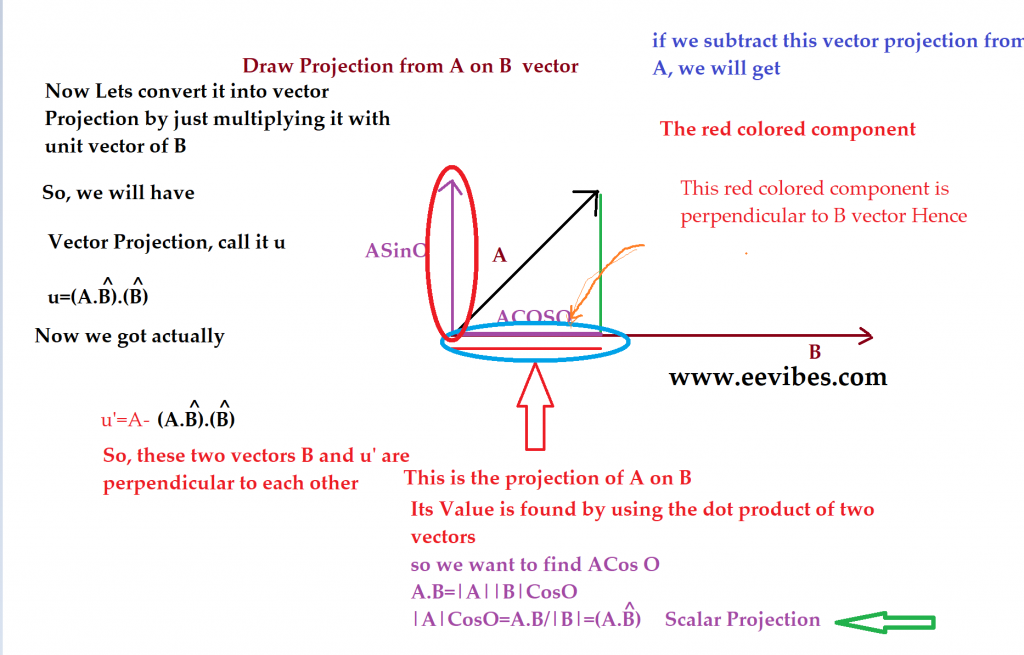
Since, by applying head to tail rule on the vectors components, we can generate the original vector A. After that we need to find the projections of one vector to another vector. This projection is subtracted from the other vector and hence these two vectors become orthogonal.
So, for two vectors A and B lets say we want to generate a new set of vectors W and Y that will be orthogonal to each other. We will assume
A=W
Then
\begin{equation}
Y=\vec{A}-(\vec{A} \cdot \hat{B}) \cdot \hat{B}
\end{equation}
Hence these two vectors will be orthogonal to each other. In order to make them orthonormal vectors just find their unit vectors, by dividing each of them with their magnitude.
Now lets just extend this idea to 3 number of vectors u,v,and w and lets assume that x,y,z will be the new orthogonal set.
so again first vector is considered as it i;
$$
\begin{gathered}
\vec{x}=\vec{u} \\
\vec{y}=\vec{v}-(\vec{v} \cdot \hat{u}) . \hat{u}
\end{gathered}
$$
Then
$$
\vec{z}=\vec{w}-(\vec{w} \cdot \vec{x}) \cdot \vec{x}-(\vec{w} \cdot \vec{y}) \cdot \vec{y}
$$
In this way we can make the given set of vectors that are linearly independent as orthogonal.
Example of Gram Schmidt Procedure
Orthonormalize the two vectors u and v where u=[1 2 2] and v=[1 0 1]
\begin{equation}
\vec{u}=\begin{aligned}
&1 \\
&2 \\
&2
\end{aligned} \quad \vec{v}=\begin{aligned}
&1 \\
&0 \\
&1
\end{aligned}
\end{equation}
If you take the dot product of these two vectors, you will see they are not orthogonal
$$
\begin{gathered}
\vec{u} \cdot \vec{v}=[1.1+2.0+2.1] \\
\vec{u} \cdot \vec{v}=3 \neq 0
\end{gathered}
$$
Let’s apply the Gram Schmidt Procedure now. Assume that the new set of vectors consists of $\vec{w}$ and $\vec{x}$
$$
\vec{w}=\vec{u}
$$
\begin{equation}
\hat{u}=\frac{1}{3}\left(\begin{array}{l}
1 \\
2 \\
2
\end{array}\right)
\end{equation}
$$
\vec{x}=\vec{v}-(\overrightarrow{\vec{x}} \cdot \hat{u}) \cdot \hat{u} \mid
$$
So, we will have
$$
\begin{aligned}
&1 \\
&0 \\
&1
\end{aligned}-\frac{1}{3}\left(\begin{array}{l}
1 \\
0 \\
1
\end{array}\right)\left(\begin{array}{l}
1 \\
2 \\
2
\end{array}\right) \frac{1}{3}\left(\begin{array}{l}
1 \\
2 \\
2
\end{array}\right)
$$
$$
\begin{aligned}
&1 \\
&0 \\
&1
\end{aligned} \frac{1}{9}[1+0+2]\left(\begin{array}{l}
1 \\
2 \\
2
\end{array}\right)
$$
$$
\begin{aligned}
&1 \\
&0-\frac{1}{3} \\
&1
\end{aligned}\left(\begin{array}{l}
1 \\
2 \\
2
\end{array}\right)
$$
$$
\begin{array}{r}
1-\frac{1}{3} \\
=0-\frac{2}{3} \\
1-\frac{2}{3}
\end{array}
$$
$$
\begin{array}{r}
\frac{2}{3} \\
\vec{x}=-\frac{2}{3}
\end{array}
$$
$\frac{1}{3}$
Now, if you take the dot product of $\vec{x}$ and $\vec{w}$.
$$
\begin{aligned}
& 1{ }^{\frac{2}{3}} \\
\vec{x} \cdot \vec{w} &=2 \cdot-\frac{2}{3} \\
& \frac{1}{3} \\
=\left[\frac{2}{3}-\frac{4}{3}+\frac{2}{3}\right]=& \frac{2-4+2}{3}=0
\end{aligned}
$$
Hence they are orthogonalized.
Video Lecture for Gram Schmidt Procedure
Here is the video lecture of Gram Schmidt Procedure
Solved Example of Gram Schmidt Procedure Simple
Here is the example of Gram Schmidt Procedure for three vectors
Also read here