Introduction
In this article you will learn about different examples for finding the eigen values and eigen vectors of matrices using different examples on MATLAB.
For the given matrix A and B, find the determinant using these two methods on MATLAB.
- Using command det(A)
- By multiplying the diagonal entries.
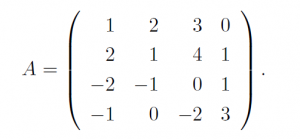
A [1 2 3 0; 2 1 4 1; -2 -1 0 1;-1 0 -2 3];
disp(‘the original matrix is A’)
disp (A)
det (A)
ans=-46
Through diagonal entries:
A=[1 2 3 0;2 1 4 1;-2 -1 0 1;-1 0 -2 3]
A(2,:)=A(2,:)-2*A(1,:)
A(3,:)=A(3,:) +2*A(1,:)
A(4,:)=A(4,:)+A(1,:)
A(3,:) = A(3,:) + A(2,:);
A(4,:) = A(4,:) – A(4,2)*A(2,:)/A(2,2)
A(4,:) = A(4,:) -A(4,3)*A(3,:)/A(3,3)
A(1,1)*A(2,2)*A(3,3)*A(4,4)
A =
1 2 3 0
2 1 4 1
-2 -1 0 1
-1 0 -2 3
A =
1 2 3 0
0 -3 -2 1
-2 -1 0 1
-1 0 -2 3
A =
1 2 3 0
0 -3 -2 1
0 3 6 1
-1 0 -2 3
A =
1 2 3 0
0 -3 -2 1
0 3 6 1
0 2 1 3
A =
1.0000 2.0000 3.0000 0
0 -3.0000 -2.0000 1.0000
0 0 4.0000 2.0000
0 0 -0.3333 3.6667
A =
1.0000 2.0000 3.0000 0
0 -3.0000 -2.0000 1.0000
0 0 4.0000 2.0000
0 0 0 3.8333
ans =
-46
 B=[1 0 2 3; -1 -2 3 2 4 -2 0 3; 1 2 0 -3];
B=[1 0 2 3; -1 -2 3 2 4 -2 0 3; 1 2 0 -3];
disp(‘the original matríx is B’)
disp (B)
det (B)
ans=-110
Through diagonal entries:
B= [1 0 2 3; -1 -2 3 2; 4 -2 0 3; 1 2 0 -3]
B(2,:)=B(2,:)+B(1,:)
B(3,:)=B(3,:) -4*B(1,:)
B(3,:)=B(3,:)- B(3,2)*B(2,:)/B(2,2)
B(4,:)=B(4,:)-B(1,:)
B(4,:) = B(4,:) – B(4,2)*B(2,:)/B(2,2)
B(4,:) = B(4,:) – B(4,3)*B(3,:)/B(3,3)
B(1,1)*B(2,2)*B(3,3)*B(4,4)
B =
1 0 2 3
-1 -2 3 2
4 -2 0 3
1 2 0 -3
B =
1 0 2 3
0 -2 5 5
4 -2 0 3
1 2 0 -3
B =
1 0 2 3
0 -2 5 5
0 -2 -8 -9
1 2 0 -3
B =
1 0 2 3
0 -2 5 5
0 0 -13 -14
1 2 0 -3
B =
1 0 2 3
0 -2 5 5
0 0 -13 -14
0 2 -2 -6
B =
1 0 2 3
0 -2 5 5
0 0 -13 -14
0 0 3 -1
B =
1.0000 0 2.0000 3.0000
0 -2.0000 5.0000 5.0000
0 0 -13.0000 -14.0000
0 0 0 -4.2308
ans =
-110
For the matrices A and B, find its characteristic polynomial, Eigen values and trace of A and B using MATLAB.
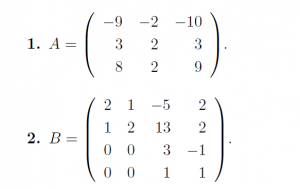
A
A=[-9 -2 -10; 3 2 3; 8 2 9];
disp(“matrix A is”)
disp(A)
disp(“characteristic polynomial of A is”)
poly(A)
disp(“Eigen values of A is”)
eig(A)
disp(“trace of B is”)
trace(A)
Answer:
Characteristic polynomial of B is
ans =
1.0000 -2.0000 -1.0000 2.0000
eigen values of A is
ans =
-1.0000
2.0000
1.0000
trace of B is
ans =
2
B
B=[2 1 -5 2; 1 2 13 2;0 0 3 -1; 0 0 1 1];
disp(“matrix B is”)
disp(B)
disp(“characteristic polynomial of B is”)
poly(B)
disp(“Eigen values of B is”)
eig(B)
disp(“trace of B is”)
trace(B)
Answer:
characteristic polynomial of B is
ans =
1 -8 23 -28 12
eigen values of B is
ans =
3.0000
1.0000
2.0000
2.0000
trace of B is
ans =
8
What do the following commands do?
Explain the output of each
- e = eig(A)
This function gives the eigon values
- [V,D] = eig(A)
V =
0.7845 0.6667 -0.7071
-0.1961 -0.3333 -0.0000
-0.5883 -0.6667 0.7071
D =
-1.0000 0 0
0 2.0000 0
0 0 1.0000
- [V,D,W] = eig(A)
V =
0.7071 -0.7071 -0.9764 -0.9764
0.7071 0.7071 0.1953 0.1953
0 0 0.0651 0.0651
0 0 0.0651 0.0651
D =
3.0000 0 0 0
0 1.0000 0 0
0 0 2.0000 0
0 0 0 2.0000
W =
0.0463 -0.0554 0 0
0.0463 0.0554 0 0
0.9265 0.0000 0.7071 -0.7071
-0.3706 -0.9969 -0.7071 0.7071
Also read here
- Eigen Values and Eigen Vectors with examples
- How to test the given vectors are linearly independent or not?
- How to diagonalize a matrix? Example of diagonalization?
- How to solve system of linear equations in Linear Algebra?
- How to perform similar matrices transformation?
- What are the nodal incidence matrices?
what are the eigen values and eigen vectors? explain with examples