Introduction to Norton Theorem
What is the Norton Theorem? Examples of Norton Theorem . Today we will talk about another important topic in electrical circuit analysis. In analyzing electrical circuit, we often encounter circuits that are beyond reach of solving with simple nodal and mesh analysis. In simple words, one cannot solve these circuits with simple methods of combining resistance and simply by using superposition method. The analysis of such circuit should be done by some special magical methods that would prove worthy by their simple and understandable rules. One such method is called NORTON’S THEOREM. This theorem can be applied for the simplification of electrical circuitry networks that are composed of linearly time-invariant resistances, voltage and current sources. It simply states that
“Any linear electrical circuit network or any complex circuit with independent current and voltage sources can be replaced by an equivalent circuit that would be composed of an independent current source and an equivalent resistance in parallel to that current source.”
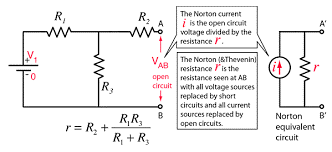
Norton’s theorem and its brother pair Thevenin’s theorem are frequently used for the study of simplification of electrical circuits. they also play a part when it comes to determining the circuit’s steady state and initial-conditions.
Background
Norton’s theorem was first introduced and independently derived by Hans Ferdinand Mayer and Edward Lawry Norton in 1926. Thus these two gentlemen should be given the credit for discovering a method which made it much easier for the student, teachers, researchers and scientists. May the souls of the departed rest in peace.
Steps to Implement NORTON’S Theorem in a Circuit
Following steps should be taken into consideration while working on Norton’s theorem.
- Initially short the load resistance. Make it disappear from the circuit.
- Norton’s current should be measured. For this measurement, in the short circuit, calculate the current flowing.
- As load resistor has already been shorted. Now apply some rules of superposition principle.
- Make the voltage sources short circuit and the current sources an open circuit.
- As we have simplified the circuit well enough. Now only resistances are left in the circuit. Calculate the equivalent resistance. This resistance would be regarded as Norton’s resistance.
- Up till now, we have obtained a current source, which is referred to as Norton’s current, an equivalent resistance, named as Norton’s resistance, and the main resistance, called the load resistance.
- Use these three components to make an equivalent circuit which will be called a Norton’s circuit diagram. First place the current source and then place both resistances in parallel to each other and also parallel to the Norton’s current source.
- We have done it. Now find the load current flowing through the load resistance. This can be easily done by using the current divider formula given as
$$
I_{\text {LOAD }}=\frac{I_{\text {NORTON }} * R_{\text {NORTON }}}{\left(R_{\text {NORTON }}+R_{\text {LOAD }}\right)}
$$
Norton’s Theorem VS Thevenin’s Theorem
As mentioned earlier, both the Thevenin’s theorem and Norton’s theorem are brother pairs. The procedure of both the methods is similar. Both theorems work their best to help the learner, simplify the circuit more easily. In fact, both the theorems offer the user a choice. The user/learner can utilize both the theorem according to his ease or feasibility.
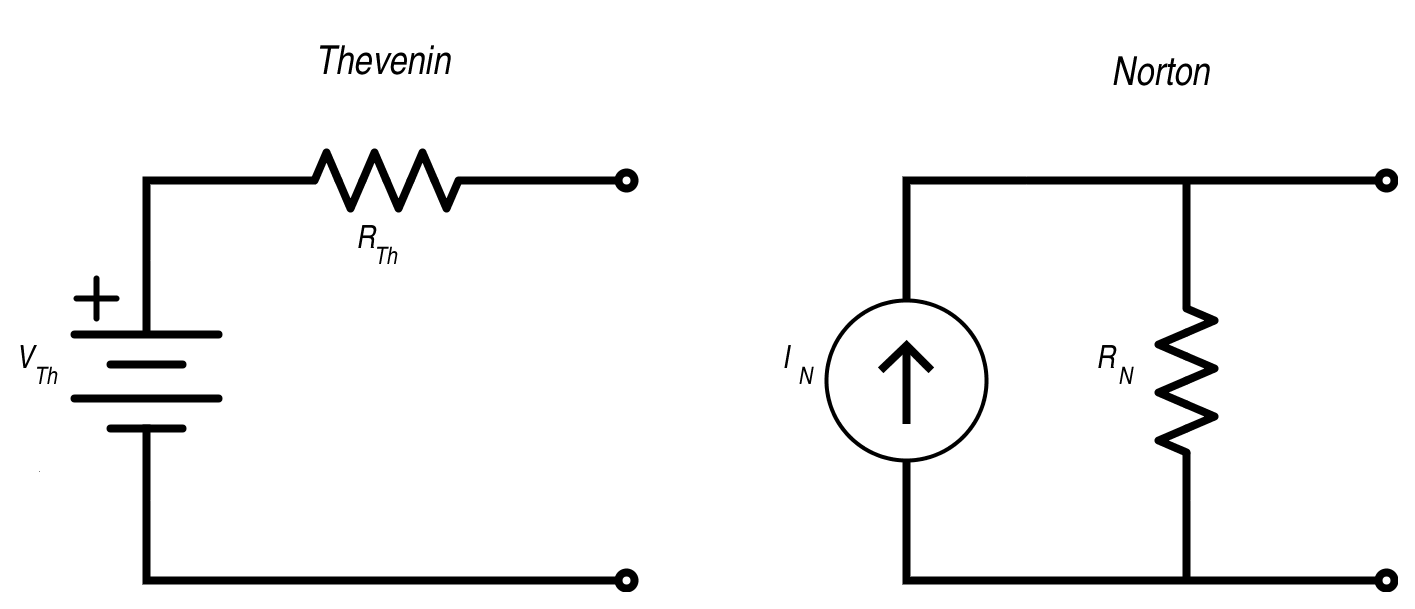
In both the theorems, we simplify the circuit and find the equivalent resistance. This step is common to both methodologies. However, in Norton’s theorem, we use the main source as an independent current source. Whereas, in Thevenin’s theorem, the main source is replaced by an independent voltage source. The other major difference in both the methods is that in Norton’s theorem, the equivalent resistance and the load resistance both are combined in parallel with the independent current source. Whereas, in Thevenin’s theorem the equivalent resistance or commonly called Thevenin’s resistance along with the load resistance is placed in series connection with the independent voltage source. One difference that would be a guess of common sense is that in Norton’s theorem, current divider formula is used. Whereas in Thevenin’s theorem voltage divider formula is used.
Both the theorems are interchangeable by following equations
$$
\begin{gathered}
R_{\text {THEVENIN }}=R_{\text {NORTON }} \\
V_{\text {THEVENIN }}=I_{\text {NORTON }} * R_{\text {NORTON }} \\
I_{\text {NORTON }}=\frac{V_{\text {THEVENIN }}}{R_{\text {THEVENIN }}}
\end{gathered}
$$
Summary of Norton’s Theorem
After studying and understanding deeply the basic principles and rules and regulation of Norton’s theorem we can conclude the whole topic into some points that would prove fruitful for everyone. These points are not the exact details of Norton’s theorem, but for better understanding of the above great topic some common solved examples of this Norton’s theorem are also given below
- Make the short resistance disappear. Disconnect it from the circuit.
- Find the equivalent resistance of the circuit by making any voltage source short and any current source open.
- Find the current flowing through the circuit
- Find the current flowing through the load resistance attached parallel to both the equivalent resistance and source.
Examples of Norton’s Theorem
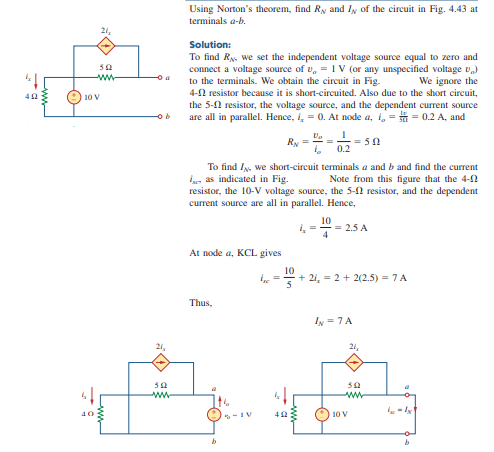
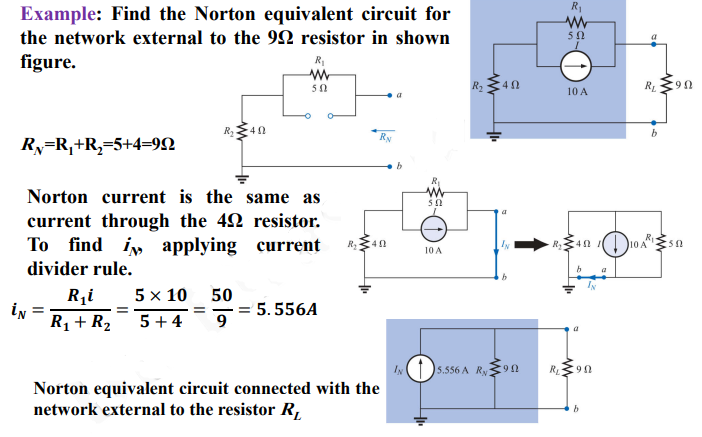
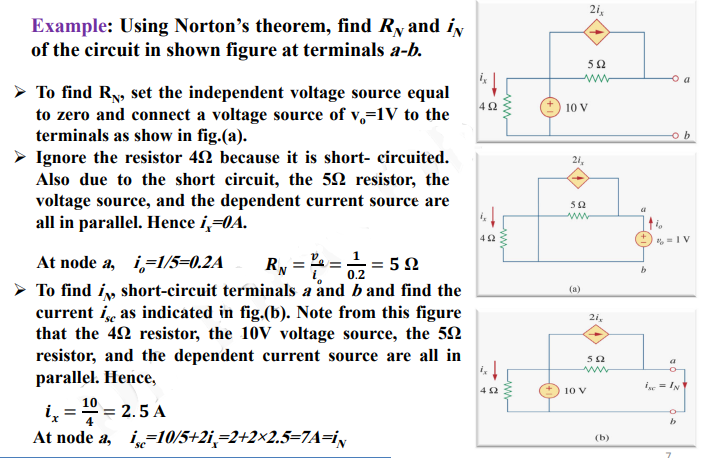
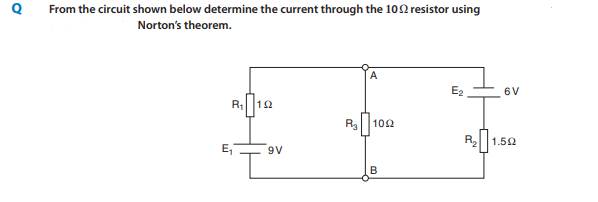
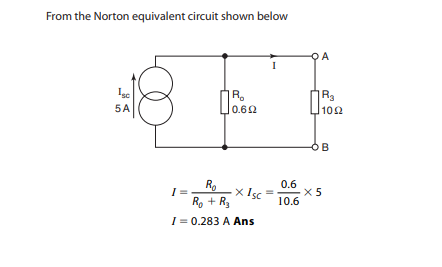
Some solved examples of Norton’s theorem are listed below for better understanding. These examples better explain the implementation of Norton’s theorem in a linear complex circuit.
Example 1
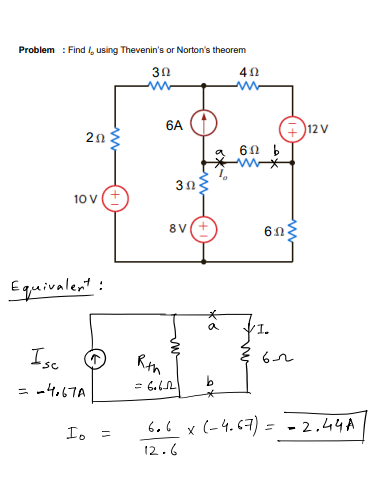
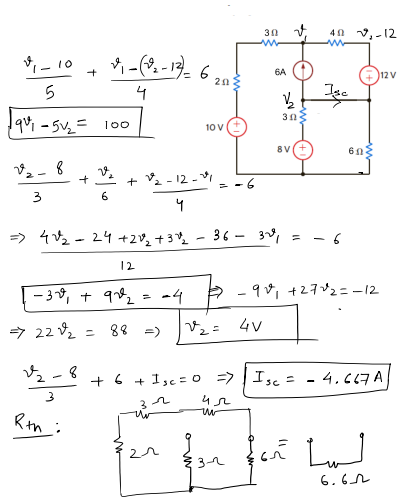
Example of Norton’s Theorem