
Introduction to Boolean Algebra
What is the Boolean Algebra? Boolean Algebra is almost similar to the ordinary algebra which includes certain number of elements, set of operations and then some unapproved axioms, postulates or theorems. Another name of the Boolean Algebra is the switching algebra since it holds the properties of bi-stable electrical switching circuits.
Huntington postulates are employed for the formal definition of Boolean Algebra. So we can say that Boolean algebra is an algebraic structure which is defined by the set of elements B with two binary operations: (+) addition and (*) multiplication. Huntington postulates must be satisfied by this algebraic structure.
Huntington Postulates
Closure Property:
This algebraic structure must be close under the operation of addition (+). Since B={0,1} so 0+0=0 0+1=1, 1+1=1. Since they all belong to set B after the addition operation that’s why it is closed under addition.
Similarly it must be closed under the operation of multiplication i.e., 1*1=1 0*1=0 0*0=0.
Identity Element
0 is the identity element with respect to addition operation since 0+x=x. While 1 is the identity element with respect to multiplication since 1.x=1.
Commutative Property
The structure commutes with respect to addition since 1+0=0+1=1 . Similarly, it also commutes with respect to multiplication i.e., x*y=y*x or 1*0=0*1=0.
Distributive Property
The algebraic structure follows the distributive property of addition over multiplication and multiplication over the addition .
a*(b+c)=(a*b)+(a*c) Distributive Property of multiplication over addition.
a+(b*c)=(a+b)*(a+c) Distributive Property of addition over multiplication .
Complement of element
For every element x, there is a complement x’ such that x+x’=1 and x.x’=0.
Distinct Element
There are at least two element x and y such that they both are distinct.
Difference Between Boolean Algebra and Ordinary Algebra
Although Boolean algebra and ordinary algebra both share the same properties there are still two properties that are not found in each other.
- Ordinary Algebra does not follow the Distributive Property of addition over multiplication.
- Just Like in ordinary algebra, we do not have the concept of additive inverse or multiplicative inverse in Boolean algebra. That’s why subtraction and division are not possible.
- There is no concept of complement in ordinary algebra.
- Ordinary algebra deals with the real numbers that can take infinite values while Boolean algebra elements can take only two values 0 or 1.
Basic Theorems and Postulates of Boolean Algebra
In the following table we have shown 6 Theorems of Boolean algebra and 4 postulates of it.

What are the Boolean Functions?
Boolean Functions are algebraic expressions formed by the Boolean variables that may appear in primed or unprimed form. So Boolean functions can take the values either 1 or 0. Consider the following Boolean function
F=x’y+z
This function will have value equal to 1 when either z=1 or x=0 and y=1. A Boolean function can be represented as a truth table where there can be 2^n possible rows where n is the number of variables.
Consider the truth table for some function F.
| x | y | z | F |
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
You can represent this function as a summation of those minterms where the function value is equal to 1. The Boolean representation of this function is:
F=x’yz’+xy’z+xyz’+xyz
Now Let’s just try to simplify this expression by using Boolean Algebra.
=y(x’z’+xz)+xy(z+z’)
since
z+z’=1
so
=y(x’z’+xz)+xy
=y[(x’z’+xz+x)]
=y[x(z+1)+x’z’]
=y[x+x’z’]
Now apply distributive law
=y(x+x’)(x+z’)
F=y(x+z’)
Which is actually the simplified expression for the above function.
The NAND and NOR gate implementation of the above function is given below.
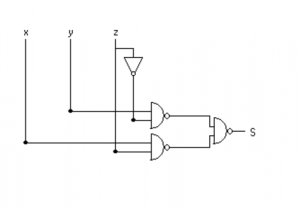
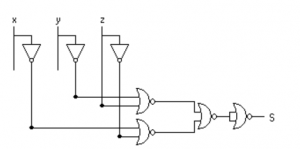
Write the following Boolean expressions in sum of products form:
F=(b + d)(a’ + b’ + c)
In order to solve this question, the best approach is to construct the Truth table for it. Then use Karnaugh map for obtaining the expression of function as a sum of products (SOPs).
| a | b | c | d | ( b +d) | (a’ + b’ + c)
|
F=( b +d)(a’ + b’ + c) |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 1 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Next step is to use k-map for deriving the function expression
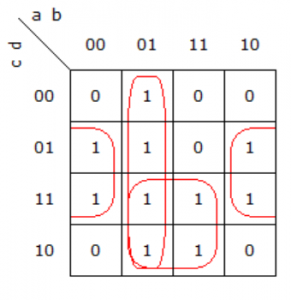
hence it will give function as :
F=a’b+bc+db’
hence the above expression has been written as sum of products form which is also called the standard form of Boolean function.
Write the following Boolean expression in product of sums form: a’b + a’c’ + abc
The first step is to construct the truth table again
| a | b | c | a’b | a’c’ | abc | F |
| 0 | 0 | 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 | 1 |
Nest step is to develop the formula of the function. One thing that is tricky here is now that you will combine zeros of the function for getting the expression of it as a product of sums expression.
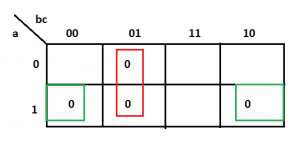
F’=b’c+ac’
In order to eliminate the complement effect, we will take another complement. hence we will have:
(F’)’=F=(b’c+ac’)’
F=(b’c)’.(ac’)’
F=(a’+c)(b+c’)
Video Lecture for Write the following Boolean expression in product of sums form: a’b + a’c’ + abc
Simplification of Boolean Functions using Boolean Algebra
Here I have solved some end problems of Moris Mano of digital logic design chapter No. 2 part 2.4
Also check
- What are the CMOS Logic Gates?
- What is the magnitude comparator circuit? Design a 3 bit magnitude comparator circuit
- What are the synchronous counters? Explain with an example.
- what are the half adder and full adder circuits?
- what are the half subtractor and full subtractor circuits?
- How to design a four bit adder-subtractor circuit?
- What are number systems in computer?
- Discuss the binary counter with parallel load? Explain its working with an example
- how to draw state diagram of sequential circuit?
- How to simplify a Boolean function using Karnaugh map (k-map)?
- What are the flip flops and registers in digital design?
- Define fan-in, fan-out, CMOS and TTL logic levels
- what is the Canonical form representation of Boolean function?
- What is difference between latches and flip flops?