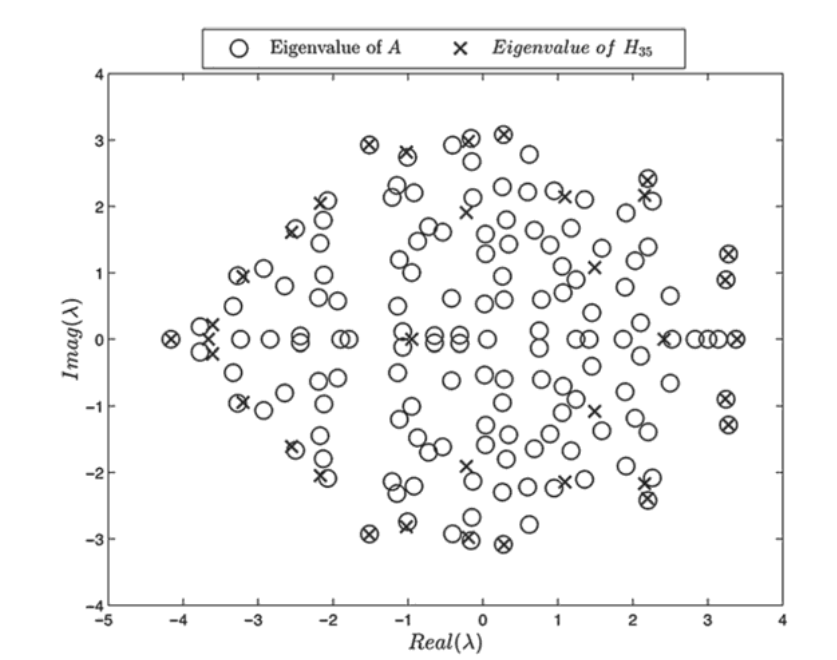
Introduction The fast Fourier transform method and ill-conditioned matrices. We have studied the problem of calculating numerical solutions of the linear algebra equation, a*x=b, where a denotes an N*N ill-conditioned coefficient matrix. It is known that Gaussian elimination methods linked Read More …