Table of Contents

Introduction

What are the Applications of Matrices in Cryptography? The science of encoding and decoding signals is known as cryptography. Cryptography is widely used in everyday life to protect tactful data such as affinity card numbers. This analysis investigates matrices and their practical use in cryptography. The goal of this research is to figure out how to generate keys by using Hill cyphers to encrypt words. This study will also investigate into the Diffie-Hellman mechanism. Matrix will be used to present the efficiency of the encryptions researched as well as more secure encryption methods.

Communication networks such as wireless, cable, and optical can convey large amounts of data, information privacy and network security are of paramount importance, as much of the data may be sensitive or confidential. Cryptography has always been a secure means of sharing data. This article will provide an overview of linear algebra, that is known as the parent matrices, as well as the research objectives, explanation of the topic, range of study, importance of conducting this research, and definitions of a few terminology.

What are the Matrices?

Matrix is a Latin term that means “womb.” A matrix is an organized arrangement of a digits or symbols in specific rows and columns encircle in a box. This research aims to provide a survey of the past of matrices and their features, as well as the different issues that are related to them and provides an overview of the literature on matrices applications written by various scholars and researchers. It examines the literature that is relevant to the research’s specific and broad aims. It discusses literature relevant to the study’s specific aims in the past studies/main review section. It also includes a critical analysis of important concerns, a summary, and gaps to be filled in the literature.

Problem description

Because of the high demand for security when sending sensitive information from one place to another or place one company to another via digital technology, cryptography is a viable solution. Because plain text attacks are a huge problem, this research will aim to overcome it by using the Diffie-Hellman method.

General Objectives

The overall goal of this study is to figure out how matrices can be used in cryptography.
To demonstrate mathematically how sensitive information can be transferred.
Matrix applications in cryptography
Using the Diffie-Hellman technique, generate a secret key.

Methodology

This topic elaborates the research techniques that will be employed in this research, as well as the data sources and computer software that will be used to compute matrices.

The data for this research methods will come from books, articles, journals, and the history of oral lectures. In this study, the MATLAB computer software will be used to solve matrices.

MATLAB stands for matrix laboratory, which is an interactive computing system meant to make solving various matrix-based scientific and engineering issues simple.

A matrix is well-ordered sequence of of some digits or symbols in particular rows and columns enclosed by brackets, titled by a capital letter and subscribed by the magnitude of its order. The fundamental challenge facing the implementation of matrices in cryptography is ordinary message attack. This research study will attempt to tackle this problem by utilizing the Diffie- Hellman technique, which is utilized to generate a secret key depends on modular exponentiation. The Diffie-Hellman method is a way for safely transferring cryptographic keys over a public network. This study will look into an encryption method that employs matrix multiplication and inverse of matrix. The following are the steps to be followed:

Conversion of alphanumeric messages to digits
Make matrices out of these numbers
Multiply the matrix by any of the private key square matrix, which will be constructed in this condition using the Diffie-Hellman technique
Data conversion from one format to another
Multiply the decoded message by the inverse of the secret key

In essence, this study will focus on matrix multiplication and secret key creation utilizing an upgraded Diffie-Hellman mechanism.

Hill uses matrix multiplication, according to [4]. Cipher works on classification of letters, in which ordinary message is divided into fixed-size classification of letters, each of which is changed into a separate category of letters. In cryptography, the Hiller cypher uses matrices. Ciphers are methods for changing plaintext into a form that can only be read and processed by those who have the key and know who it is intended for. Assigning mathematical digits from 1-26 to the letters and sending data to a cord of integers is a frequent approach to deliver coded messages. The problem is that by analyzing the frequency of numbers that appear in the coded messages, these codes can be easily broken.

The mathematical operation is given by: 𝑚𝑜𝑑 26 (𝐴𝐵) = 𝐶

𝑤ℎ𝑒𝑟𝑒 𝐵 𝑖𝑠 𝑡ℎ𝑒 𝑚𝑒𝑠𝑠𝑎𝑔𝑒, 𝐴 𝑖𝑠 𝑡ℎ𝑒 𝑒𝑛𝑐𝑜𝑑𝑖𝑛𝑔 𝑚𝑎𝑡𝑟𝑖𝑥 𝑎𝑛𝑑 𝐶 𝑖𝑠 𝑡ℎ𝑒 𝑒𝑛𝑐𝑟𝑦𝑝𝑡𝑒𝑑 𝑚𝑎𝑡𝑟𝑖𝑥. On recipient side for the individual to get the real message the given process is used

𝐵 = 𝐴⁻¹𝐶

An introduction to elliptic curve cryptography focuses on the Fp kind of elliptic curve, which is produced over a finite field. In cryptography, the elliptic group mod p, where p is a prime number, is a topic of great interest. It’s defined as follows:

$4 \alpha^{3}+27 \beta^{2}(\bmod p) \neq 0$
Ep $(\alpha, \beta)$ is an elliptic group mod $p$ whose elements $(x, y)$ are non-negative integer pairs less than $p$ satisfying:
$$
\mathrm{y}^{2}=\left(x^{3}+\alpha x+\beta\right) \bmod p
$$

For elliptic curve encryption and decryption, this paper used the Elgamal cryptosystem. It then goes on to describe an Elgamal cryptosystem and how to use one.

Convert the plaintext message m into an x-y point pm.
The cypher text of point pm is encrypted and then decrypted.

Communication between Alice and Bob was one of the examples examined in this study. If we have an ovate curve E explained over a limited field Fp, and E and a point p E are candidly known as the embedded system mm pm, which embeds ordinary text on elliptic curve E, then when Alice wants to liaise privately with Bob, they do the following:

Bob subtracts the first component of the pair from the second to decode the message by getting:

\begin{equation}
\mathrm{PiI}(\mathrm{ap}) \mathrm{a}(\mathrm{Ip})=\mathrm{pi}+\mathrm{Iap}=\mathrm{pi}
\end{equation}

and then reverses the operation. This method both sender and receiver of message requires to know the following:

Mapping methodology

Step1:

Transform alphanumeric characters into elliptic curve points

\begin{equation}
\left\lfloor\left(p_{1}\left(x_{1}, y_{1}\right), p_{2}\left(x_{2}, y_{2}\right), p_{3}\left(x_{3}, y_{3}\right) \ldots \ldots \ldots \ldots \ldots \ldots p_{n}\left(x_{n}, y_{n}\right)\right\rfloor\right.
\end{equation}

The initial length n is regarded as m. The points have been padded with to indicate space if n is not divisible by 3.

Step2:

𝑝1 𝑝2 𝑝3 … … 𝑝𝑟

𝑚 = [𝑝𝑟+1 𝑝𝑟+2 𝑝𝑟+3… … 𝑝𝑠]

𝑝𝑠+1 𝑝𝑠+2 𝑝𝑠+3… … . 𝑝𝑛

With r=n/3 and s =2n/3

Step 3: Using addition and doubling of points, compute the following: 𝑄 = 𝐴𝑀

Step 4: Using elliptic curve decryption techniques and the universe of matrices, this message may be extracted from the encoded data.

the result set of point is $s=\left[Q_{1}\left(x_{1}, y_{1}\right), Q_{2}\left(x_{2}, y_{2}\right)\right.$ $\left.Q_{n}\left(x_{n}, y_{n}\right)\right]$

Many cryptosystems were created to prevent unauthorized access to data, according to [3,] yet some are relatively insecure. The Hill cypher algorithm is described as the most efficient cryptosystem in this study. This research tackled the issues of matrices that are not admitting an addictive and multiplicative inverse by changing the way key matrices are handled and making all matrices invertible. It also resolved the known issue of pair and cypher’s text by producing a new key matrix for each encrypted block of plaintext using SHA-512. This document also elaborates how to solve all Hill’s difficulties.

The first method is to solve the non-invertible matrices problem, which allows us to utilize the second method. This research divides encryption systems into two types: symmetric and asymmetric. Symmetric encryption/secret key/ single key employs the same key used by the sender to encrypt and decode data on the receiving end. A secure method for moving a secret key must be employed in symmetric encryption. The asymmetric encryption approach is slow and difficult to use. Hiller cypher is defined as the application of modular linear algebra to cryptography in this study. Lester S. Hill devised the Hill cypher in 1929. The concept of Hill was related to multiplications of matrices.

$c=k \times x \bmod p$
1
Where c represents cipher text, $x$ represents plain text, $k$ represents key matrix, $p$ is the modular value
$$
x=k \times c \bmod p
$$
Following are the issues of Hill cypher:
i. Because encrypted text cannot be deciphered, there are no invertible matrices.
ii. Plaintext attack: Because of the linear nature of the Hill cypher, the cryptosystem can be defeated using a known plaintext assault.

Findings

We use a matrix to encrypt an alphanumeric message in the following steps:

Convert an alphanumeric message to a numerical message
Make a matrix out of these numbers.
Create a secret key.
To decode the message, use a secret key.
Multiply it with the inverse of the secret key to decode an encoded message

Procedure:

1: Convert the alphanumeric message to a number

A number is allocated to each alphabetic letter. In this part we’ll employ the given correspondence, in which the alphabets from A to Z correspond to numbers 1 to 20, and punctuation is ignored while number 27 represents the space.

Make a matrix out of the numbers

Because the secret key will be multiplied by the created matrix, it has the given property. If A and B are two matrices represented by AB, then the number of columns in the first matrix must match the number of rows in the second matrix, i.e., if A is mn and B is np, then C=AB is defined as mp matrix.

Generate secret key

A secret key can be defined as the single key which we used to decrypt and encrypt our data and can be shared as well between two communicating parties privately. The fact that this secret key must be communicated via an external mechanism separate from the communication channel over which the encrypted text is transmitted is a major issue. It is simple to decrypt the encoded message using this secret message. Due to the need for confidentiality, this study leverages the Diffie-Helman key exchange, which creates a shared secret. They both were wish to share a secret key for a proportioned cypher, but their only mode of transmission is unsafe. A solution to this is the Diffie–Helman key exchange. It proceeds as follows:

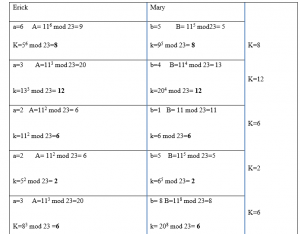
Step 1: Mary and Erick must second that on a nonzero integer g and a prime digit p, which will be referred to as the generator. The p and g values have been made public and can be exchanged via email.

Step 2: Erick chooses a secret integer ‘a’ that he does not reveal to anyone, while Mary chooses a secret integer ‘b’.

𝐴 ≡ 𝑔𝑎 𝑚𝑜𝑑 𝑝 ( 𝑒𝑟𝑖𝑐𝑘) 𝐵 ≡ 𝑔𝑏 𝑚𝑜𝑑 𝑝 (𝑚𝑎𝑟𝑦)

Erick and Marry arrive at the give result:

Step 3: Later, Erick and Marry exchange two letters A and B, with Erick send letter A to Mary and Mary send letter B to Erick. As these letters are communicated by an email address, because they can be easily broken by a hacker of any third-party as they cannot be deemed private.

Step 4: Finally, Erick and Mary compute using their secret integers.

𝑘 ≡ 𝐵𝑎𝑚𝑜𝑑 𝑝 ( 𝑒𝑟𝑖𝑐𝑘 ) 𝑘 ≡ 𝐴𝑏𝑚𝑜𝑑 𝑝 (𝑚𝑎𝑟𝑦)

4: Because the created key is secret, it may be used to encrypt messages delivered to recipients via public devices. Multiplying the matrix message by the secret key, the message is encoded.

5: The recipient has the secret key, he or she can decode the encrypted communication using the inverse of the secret key. We know that if we have two matrices A and B, we can multiply them using the following formula:

𝐴. 𝐵 = 𝐶

𝐴 = 𝐶. 𝐵⁻¹

Illustration

Mary and Erick intended to send each other ATM numbers through mail, but they were apprehensive that a third-party hacker named Denis would be involved. As a result, while transmitting ATM numbers, they choose for matrices.

The ATM number is 5314 9402 3890 4384.

To use the secret key, they are needed to be agree on this, but because they were so far away, they could only do so by utilizing public transportation. Because the data was so sensitive, it was vital to disclose this secret key as safely as possible.

Generated secret key via secure method of sharing key is

$\square^{-1}=\left[\begin{array}{cccc}3 / 34 & 1 / 17 & -1 / 17 & -1 / 34 \\ -138 / 667 & 61 / 697 & 75 / 697 & -39 / 697 \\ 23 / 7667 & 106 / 7667 & -361 / 7667 & 355 / 7667 \\ 1260 / 7667 & -860 / 7667 & -109 / 7667 & 447 / 7667\end{array}\right.$
$$
\square=\left[\begin{array}{rrrr}
5 & 9 & 3 & 4 \\
3 & 4 & 6 & 3 \\
1 & 0 & 9 & 8 \\
4 & 2 & 0 & 4
\end{array}\right]
$$
$A^{-1} X=M$ to decode the encoded matrix $x$
Where $\mathrm{A}=$ secret key
$M=$ information to be encoded $X=$ encoded matrix
$\mathrm{T}$
$X=\left[\begin{array}{cccccccccccc}8 & 6 & 1 & 9 & 5 & 9 & 3 & 4 & 95 & 114 & 69 & 94 \\ 12 & 13 & 12 & 9 & 9 & 3 & 4 & 6 & 3_{7-\ulcorner} 147 & 178 & 222 & 219_{\urcorner} \\ 6 & 16 & 3 & 10 & 1 & 0 & 9 & 8 & 145 & 150 & 141 & 160 \\ 2 & 12 & 21 & 13 & 4 & 2 & 0 & 4 & 119 & 92 & 267 & 264\end{array}\right.$

Mary receives the encrypted communication through public transportation. To receive the intended message, Mary must decode the message given by Erick by multiplying the encoded message with the inverse of A.

Mary was able to obtain the exact ATM number in a safe mean by multiplying the encrypted text with an inverse. Denis, who is the third-party hacker, is unable to access the data given to Mary because he lacks the secret key.

Second illustration

Kenyan military and Al-Shabab are at war. Kenyan military personnel are coherent into services. One unit could want to send a secure message to another troop. Let’s pretend the message says ATTACK IS TONIGHT.

Conclusion

Matrix cryptography can be used to protect data transfer as the insecurity of sending sensitive data from one person to another grows. The Diffie-Helman mechanism was employed in this study to come up with innovative ways to send a secret key via public transit.

Recommendation

In future research initiatives, advanced encryption techniques such as Encryption Data Standard, leman should be used (RSA). This will help to reduce cybercrime, notably the hacking of sensitive data sent between two parties.