
Introduction
In this article you will get the idea of Application of Linear Algebra in Computer Graphics. Computer Graphics, matrices used to represent many different types of data. Games that include 2D or 3D graphics rely on other matrix applications to show the location of the game and the characters in the game. In this paper, the Linear Algebra process in Computer Graphics is discussed with examples from different areas of Computer Graphics.
Methodology
The first use of Linear Algebra can be seen in the polygonal structure of 3D characters and space in computer games and other 3D graphics applications. Polygons are used to make images look three-dimensional because of their geometric structures. Most of the time, this is done by dividing the object into smaller and smaller polygons where the given smaller parts are triangular. This makes the production of 3D objects part of the distribution process of polygons. A simple example of the use of polygons in 3D images in the form of object frame.
The second process in 3D images is called animation. This process describes the relationship between 3D objects in a three-dimensional space over time. This can be done in many different ways such as key frames, inverse kinematics and motion capture.
What is Motion capture?
It is a 3D animation using sensors or cameras to capture the movement of an object or person in the real world.
What is Inverse kinematics?
is a powerful tool for creating games or movies that make it possible to calculate precise locations of an integrated system in order to finally reach a certain goal. This is done in the movies to capture the facial expressions of the characters that will be used in animation to show those expressions to the provocative characters.
The third process in 3D images is called 3D rendering. The 3D rendering uses a 3D string model of an object or object to produce a animated scene or 2D image from a location. This is done using two functions. The first is the transport function, which means how much light is lit on the surface of the surface, where the light is coming from, and how strong the light source is. The second function is called scattering which determines how the surface area interacts with light. These two functions are required to render 3D models in CAD animation, or even physics and weather animation etc.
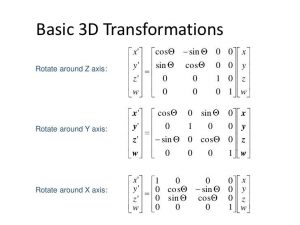
Rotation:
When working with 3D rotation you should consider which axis you would like to render.
Scaling
In some cases it may be necessary for the item to be resized to the same coordinate. The axes are then turned into different scales. As mentioned earlier to measure a 2D point in x direction with Sx and in y direction S we need to convert it as:
To achieve this, we use representation of the form matrix,
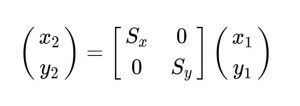
3D graphics can be divided into the following different processes:
The first to model the surface of the object was to represent a group of points in the 3D space. This process is done with the help of modeling software, or by using special 3D scanners. However, the result remains a collection of points in 3D space. These are vector points in Linear Algebra, where Linear Algebra processes such as rotation, rotation and measurement can be used.
Application of 3D modeling:
- 3D models have several uses in computer-assisted design (CAD) for engineering purposes.
- In advanced scanning techniques with the help of MRI.
- 3D organ models can be created that can help diagnose and assist in treating patients.
- 3D protein models can aid cancer research. In this case.
- 3D models that are often used in movies and TV shows to represent characters as well as objects.
- Facial expressions of actors to be used in animation to depict those expressions on animated characters.
- Characters or objects can be made realistic with advanced modeling techniques.
- In the Robotics to calculate the path required for a robot in order to successfully perform a maneuver and task.
- Video games uses analog to control movement. It adds and subtract vector to calculate player speed and space and movements.
Conclusion:
Linear Algebra is used in many different ways in computer graphics. Computer image architecture uses many functionality and theories in Linear Algebra to assist with 2D / 3D models, animation and rendering. There are many uses for 3D wire frames such as viewing a model at any angle or using it to analyze distances between edges and corners. it is used in computer games. 3D object rendering is being used in movies to show objects.
Also read here
- what are the row spaces, column spaces and null spaces in Linear Algebra?
- How to solve system of linear equations in Linear Algebra?
- what is the vector space in linear algebra? vector space example
- How to test the given vectors are linearly independent or not?
- What are the matrices and their types ?
- Finding Eigen Values and Eigen Vectors using MATLAB
- How to diagonalize a matrix? Example of diagonalization
- What are the shortcuts for finding the determinant of a matrix?
- What are the Block Matrices?
- what are the examples of scalar and vector quantities?
- How to perform similar matrices transformation?
- How to find the basis of a vector space V?
- what are the eigen values and eigen vectors? explain with examples
- What are the nodal incidence matrices?
- What is the span of a vector space?
- Study of Linear Transformation and its Application