What are number systems?

What are the Different Types of Number Systems in Computing? Usually we humans are more comfortable with decimal numbers (base 10). But in computer system we have other types that are used as per the requirement. Computer understands only the logic 0 and 1. This logical representation is called binary representation. In this form, the base is 2. Similarly, there is a variety of number systems that has different applications in computers. For example ASCII codes are used for representing alphanumeric data and special characters in computers. Hex numbers are used for representing addresses of memory locations as they are the compact form of binary numbers.

If we make a list of commonly known number systems then we have

How to determine the range for base ‘n’?

The range is determined using formula 0 to n-1.

So, for base 10 the range is 0 to (10-1=9).

So, what are the number systems? There are different types and each type is discussed in detail here.

Binary numbers

Binary numbers need only bit 1 and 0 for their representation. Any decimal number can be represented in binary. Thus if we want to convert a decimal number 23 into binary we will divide it by 2 as shown in the figure below

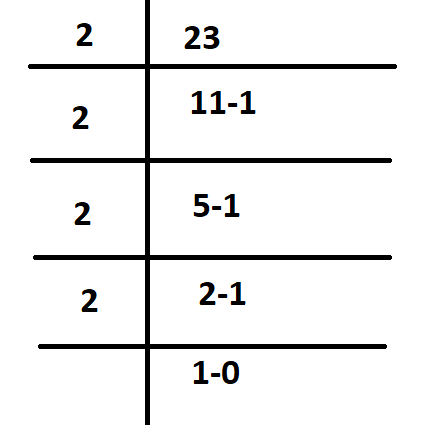
The binary equivalent of 23 is (10111). Here 23 is divided by 2 and the remainder is written after the dash. Then 11 is divided by 2 and again the remainder 1 is written and so on until the quotient is less than 2 is obtained. The left most bit is called the MSB (Most Significant Bit) and the right most bit is called LSB( Least Significant Bit).

Conversion from binary to decimal

This is basically the reverse procedure of the above one. Here we add the binary weights of each bit and then the resultant is the decimal number. Lets do an example for understanding this.

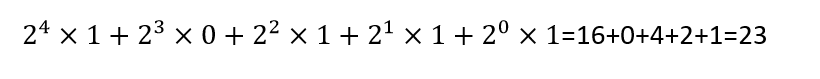
Start multiplying the LSB with 2 raise to power 0 and MSB with 2 raise to power m-1, where m is the total number of bits in the binary expression.

Octal Numbers

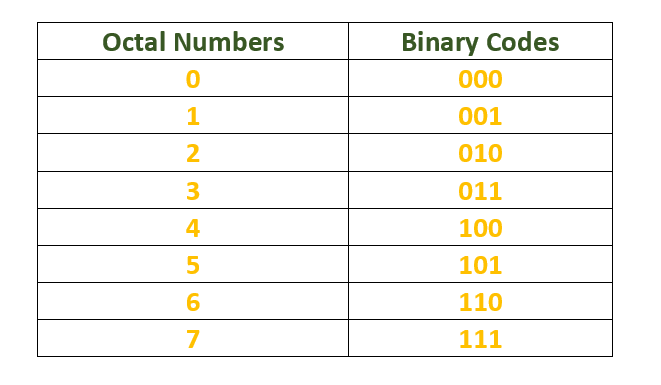
Octal Numbers have base 8 and their range is from 0 to 7. 3 bits are needed for representing each octal digit into binary. The binary code for octal numbers is shown below.

How to convert a decimal Number into octal?

If we want to convert any decimal number into octal number then we divide it with 8 just like we did in case of binary numbers.

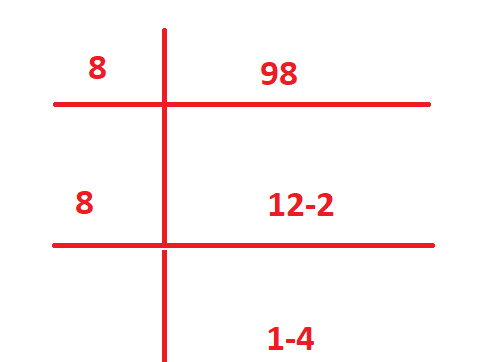
So 98 in decimal is equal to 142 in octal. Here each digit is less than 8 (1<8, 4<8, 2<8).

Conversion From octal to decimal

The same procedure is followed while converting an octal number into decimal. But here the base is 8 is multiplied with each digit of octal representation.

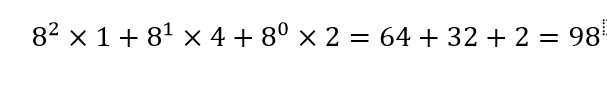
Hexadecimal Numbers

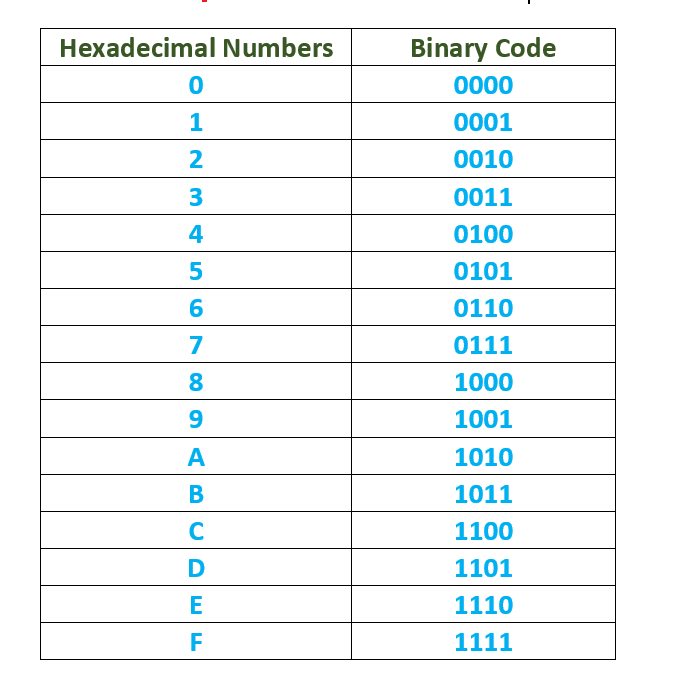
The hexadecimal numbers have base 16. Their range is from 0 to 15 (F). Four bits are required for representing each hex digit. The following table shows the binary equivalent of each hex digit.

representation of hex numbers into binary

As we have mentioned already that the hex representation is the compact form of binary numbers so if we have some binary expression as

0000 1110 1101 0101 0010 1010 0101 0010

Then its hex can be written by combining 4-bits from Right side.

0010=2

0101=5

1010=A

0101=5

1101=D

1110=E

0000=0

So its Hex representation is

0ED5A52H.

Notice that we write H at the end of hex representation usually.

How to convert a decimal number into Hex?

Convert 900 into Hex.

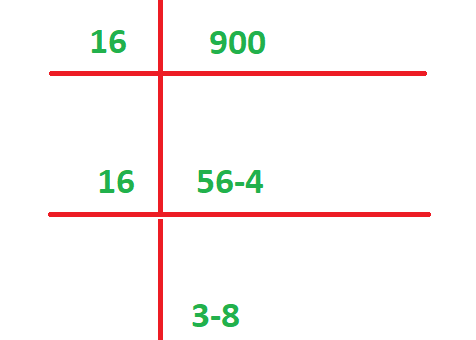
900=384 in hex.

How to convert a Hex into decimal number?

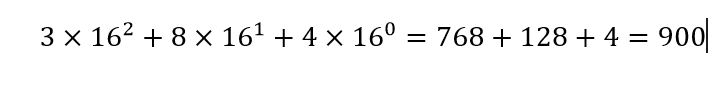
BCD (Binary Coded Decimals)

In this representation, binary codes are assigned to decimal numbers. Each decimal digit needs four bits for its binary representation as shown in the following table.

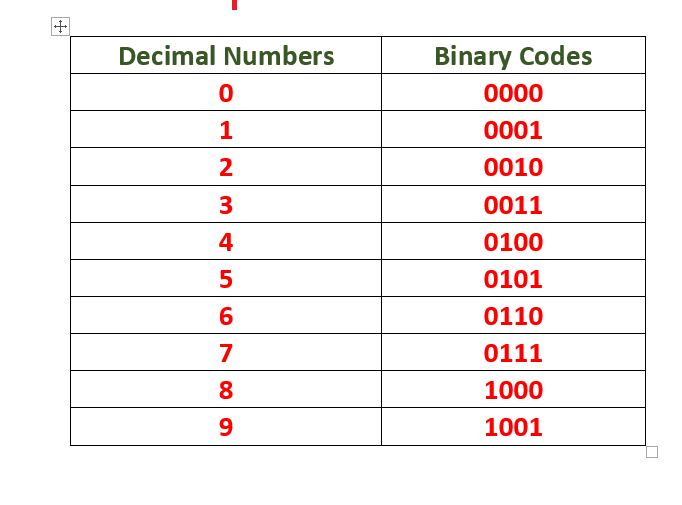
Important Notes:

If we want to convert a decimal number into any base ‘n’ we divide that number with base n and note down the remainders at each step.
If we want to convert any number represented in base ‘n’ we multiply each digit of that number with weights of that base ‘n’.

Is it possible to convert an octal number into hexadecimal representation ?

There are two ways to convert an octal number into hex

The first one is to convert that octal number into decimal, and then decimal to hex.

The second approach is by combining bits of its binary representation.

Example

Convert 352 (in octal) into hex?

3=011

5=101

2=010

so, 352=011 101 010

As we know that each hex digit needs 4 bits for its representation so we will start combining 4 bits from right most and then append zeros for completing the number of bits on left side.

0000 1110 1010

0000=0

1110=E

1010=A

so 352 in octal is equal to 0EA in Hex.

video lecture for numbers in computer systems

https://www.youtube.com/watch?v=z5YfUNYwJSg

Complement of a number

The complement of a number has a significant role in performing the subtraction of a number. In order to find the negative of a number we take complement in that particular base. There are two types of a complement in base ‘r’.

Radix complement
Diminishes Radix complement

Radix complement

For any integer N in base ‘r’ having ‘n’ no. of digits, the radix complement is given as

rⁿ-N

This is also called the r’s complement of a number. In case of a decimal number N=1234 the r’s complement is 10⁴-1234=8766. Another way to find the 10’s complement of a decimal is to subtract the right most digit (if it is not zero, otherwise look for the next non zero digit) from 10 while all other digits are subtracted from 9.

999910

23456 –

__________

76544

__________

Similarly

99910

44150-

________

55850

________

Diminished Radix complement

This form of complement is also knows as the (r-1)’s complement. If An integer N has n bits in base r, then (r-1)’s complement is found by using the following formula

(rⁿ-1)-N

The following lecture explains multiple examples of complement and its use while subtracting two numbers.

Video lecture for finding the complement of a number

https://www.youtube.com/watch?v=z26DA3IAx-Q

2’s complement of a number

Two’s complement can be easily calculated using online 2’s complement calculator

https://www.youtube.com/watch?v=pcxqOHq4yA4

What are the Different Types of Number Systems in Computing?