
Binary Arithmetic
What is binary arithmetic? Binary arithmetic is very interesting and easy to understand once you are familiar with its rules. In computer we need to perform addition, subtraction, multiplication, and division many times. Sometimes while calculating the addresses or sometimes while determining the value of counters and timers we need to perform addition and subtraction. Similarly analog to digital conversion demands to perform the division. Lets study about what is binary arithmetic in detail with examples.
Binary Addition
The addition of binary addition follows the following rules:
- 0+0=0
- 0+1=1
- 1+1=0, carry=1
If we follow these simple rules, we can add any numbers of binary numbers easily.
Examples
Lets do some examples for understanding how binary numbers are added.
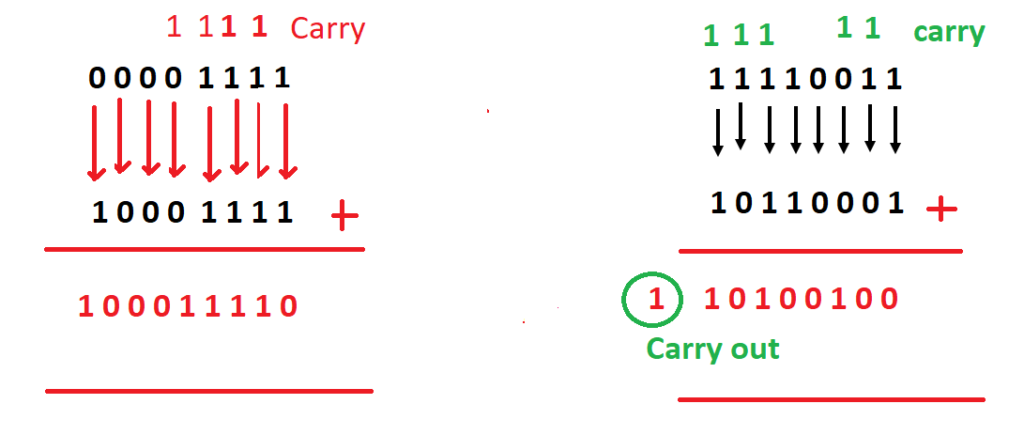
Here the addition of two binary numbers is shown. We can add two or more binary numbers using the same method. Whenever there is a carry out of MSB then the resultant is greater than the range of given bits available.
Binary Subtraction
The following rules are used while performing the binary subtraction
- 0-0=0
- 1-0=0
- 1-1=0
- 0-1=1 borrow 1
Examples
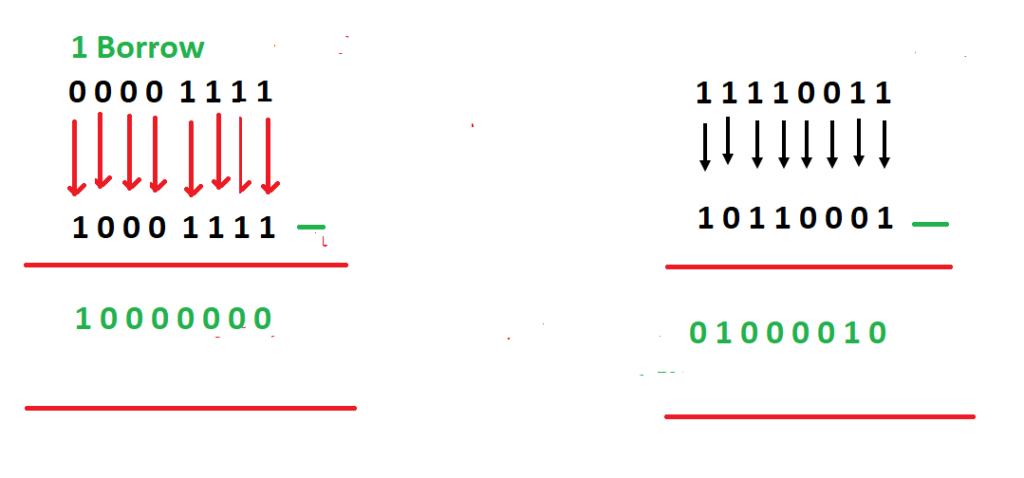
Lets have a more closer look of these two examples. Lets first consider the subtraction of 10001111 from 00001111. If we say A=00001111 and B=00001111. We have performed A-B. As both numbers are 8 bits we can treat them as signed integers. The decimal value of A= 15 (since MSB=0 so it is a positive number). As the MSB of B=1 , so it is a negative number. For Finding its decimal equivalent, we need to take its 2’s complement.
https://www.youtube.com/watch?v=pcxqOHq4yA4
1 1 1 1 1 1 1 2
1 0 0 0 1 1 1 1 __
____________________
0 1 1 1 0 0 0 1
____________________
Now convert it into decimals (0 1 1 1 0 0 0 1=113)
Now, append negative sign before it for making it a negative number. B=-113
A-B= (15)- (-113)
15+113=128
which is equal to the decimal equivalent of the resultant (1000 0000).
The same approach can be taken for interpreting the resultant of second example. One more example is shown below:
C=1 0 0 0 0 1 1 1
D=1 1 1 1 1 0 0 1 –
_________________
1 0 0 0 1 1 1 0 (C-D) =(-114) verify it by using 2’s complement !!!!
__________________
unsigned interpretation
C=135, D=249, C-D=135-249=-114
C=10000111 -ve number
2’s complement of D= 0 0 0 0 0 1 1 1 (means we have found the negative of D)
1 1 1 1 1 1 1 2
1 1 1 1 1 0 0 1
_______________
0 0 0 0 0 0 1 1 1 (-D)
_______________
add this -ve D into C
0 0 0 0 0 1 1 1
1 0 0 0 0 1 1 1 +
__________
1 0 0 0 1 1 1 0 =(-114)
__________
signed interpretation
C=-121
D=-7
so, C-D=(-121)-(-7)
-121+7=-114
Lets verify the resultant.
1 0 1 0 1 1 1 0 (-ve number)
1 1 1 1 1 1 2
1 0 0 0 1 1 1 0 –
________________
0 1 1 1 0 0 1 0
________________
More examples for subtraction
1 0 1 0 (10) 1 1 0 1 0 0 (52)
1 1 1- (7) 0 1 1 00 1 (25)-
____________ _______________
0 0 1 1 (3) 0 1 1 0 1 1 (27)
____________ ________________
Binary Multiplication
The multiplication of binary numbers is very easy.
- 0X0=0
- 0X1=0
- 1X1=1
Examples
1 1 0 0 (12)
0 1 1 (3) X
___________________
1 1 0 0
1 1 0 0 X
0 0 0 0 X X
___________________
1 0 0 1 0 0 (36)
___________________

Binary numbers Division
Dividing two binary numbers involves subtraction as major part. The following rules are adopted while performing the division of binary numbers.
- 0/0=0
- 0/1=0
- 1/1=1
- 1/0 =infinity
Examples
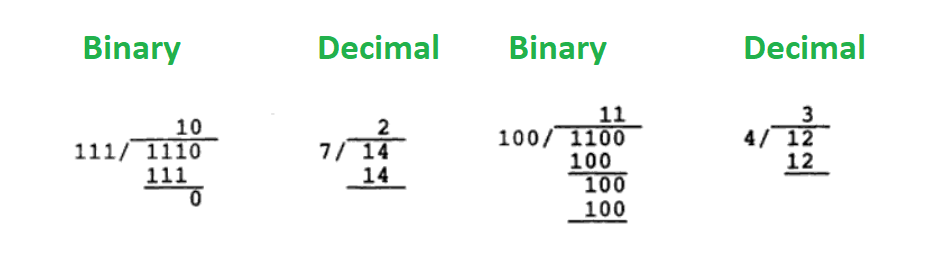
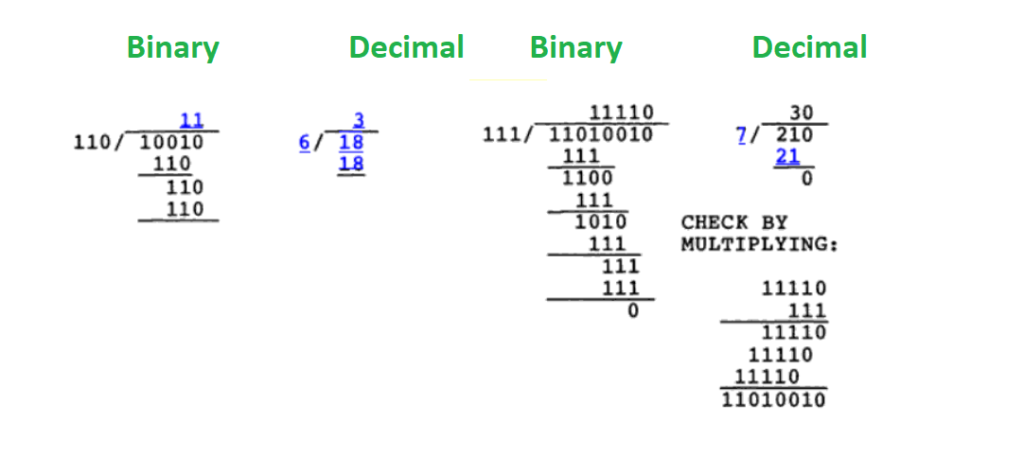
One easy trick for binary numbers division is: First convert both the dividend and the divisor into decimal. Since decimal numbers division is easy to do as compared to binary. After performing the decimal division, find its equivalent in binary.
How to divide in binary more examples
The binary division is a lot simpler than the decimal division when you recall the accompanying division rules. The primary guidelines of the binary division include:
1÷1 = 1
1÷0 = Meaningless
0÷1 = 0
0÷0 = Meaningless
Like the decimal number framework, the binary division is comparable, which follows the four-venture measure:
Gap
Increase
Take away
Cut down
Significant Note: Binary division follows the long division strategy to locate the resultant in a simple manner.
Question: Solve 01111100 ÷ 0010
Arrangement:
Given
01111100 ÷ 0010
Here the profit is 01111100, and the divisor is 0010
Eliminate the zero’s in the Most Significant Bit in both the profit and divisor, that doesn’t change the estimation of the number.
So the profit gets 1111100, and the divisor gets 10.
Presently, utilize the long division technique.


Now, on the off chance that we need a whole number (entire number) answer in remainder furthermore, leftover portion structure, we’ll compose it as 101 r 1001. That is 5 leftover portion 9 in decimal. We can likewise compose that as 101 1001/1100 (5 9/12 decimal) by putting the rest of the divisor. That portion can be decreased to 101 11/100 (5 3/4 decimal) by isolating the numerator and denominator by 3. In the event that we need a “radix” answer – what could be compared to 5.75 – we can proceed with the long division measure by adding a radix point (the binary likeness a decimal point) and some following zeros on the profit. We’ll put a radix point in the remainder straightforwardly over the divisor’s too:

Presently we can proceed with the long division measure. We convey down the following digit (the first of our following zeros) and check: Can 1100 go into 10010? Note that for the deductions, we’ll overlook the radix point. Once more, the appropriate response is indeed, so we record a 1 (this one is to one side of the radix point in the remainder) and take away:

We’ll convey down the following digit once again and move over another place. Can 1100 go into 1100? Once more, the appropriate response is truly, so we record another 1 and take away. Since the consequence of this deduction is zero, we’re done and we have an accurate answer:

Similarly likewise with decimal, a few qualities won’t partition uniformly, and we’ll get a rehashing partial part. We can stop whenever, yet understand that we’ve just discovered a guess, not an accurate worth. One last note: If the divisor (the 1100 in this model) has a radix point in it, move the radix focuses in BOTH the profit and divisor to the privilege an equivalent number of spots adequate to eliminate it from the divisor. For instance, to isolate 11001.1 by 11.001, first move both radix focuses right 3 spots (you’ll need to add zeros to the profit.) Then separation 11001100 by 11001.
Also read here:
- What are the CMOS Logic Gates?
- What is the magnitude comparator circuit? Design a 3 bit magnitude comparator circuit
- What are the synchronous counters? Explain with an example.
- what are the half adder and full adder circuits?
- what are the half subtractor and full subtractor circuits?
- How to design a four bit adder-subtractor circuit?
- What are number systems in computer?
- Discuss the binary counter with parallel load? Explain its working with an example
- how to draw state diagram of sequential circuit?
- How to simplify a Boolean function using Karnaugh map (k-map)?
- What are the flip flops and registers in digital design?
- Define fan-in, fan-out, CMOS and TTL logic levels
- what is the Canonical form representation of Boolean function?
- What is difference between latches and flip flops?
One thought on “What is binary arithmetic? How to add, subtract, multiply and divide two binary numbers?”