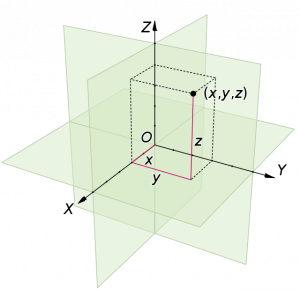
What is the Euclidean Vector? The calculative cycle for estimating internal and external places is known as Euclidean space. The Euclidean space is the name given to this computation. It’s also used in Euclidean distance calculations. It’s also used in a variety of fields and applications. It is commonly used to characterize calculations and has a wide range of applicability in science. The Euclidean space and its practical application have been discovered and discussed in this paper in the possibility of the aforementioned view. The main goal is to focus on and educate the relevant topic while also investigating the computational feasibility by discussing previous work.
Introduction
Euclidean space is the variety of tuples or focuses which can be utilized for the investigation of the limits in the information measurements for various reason and in various areas. It has been broadly utilized with the correspondence framework. The correspondence between the hubs and the appropriateness with the most limited course has stressed the examination improvement in this field. There are a few applications including the picture acknowledgment, quality articulation profiles, plan and displaying, radio wire and correspondence frameworks. It is likewise wide materialness in various designing applications. additionally utilized the distance space in various ways and demonstrated the appropriateness of the superior exactness and better recognition system . They have utilized these distance spaces with the bunching strategies. The appropriateness can be reached out as far as the transmission framework and the underlying block accommodation for allowing the source and recipient similar pieces of information or the hubs. It is also utilized for the autocorrelation properties.
The primary targets of this paper are as per the following:
- To explore and break down the areas of convenience for the application advancement and the improvement in the outcomes.
- Center around associated study effort in a similar space in light of computational viewpoints.
- To talk about the crucial angles with the benefits and gives the answers for the holes.
Literature review
In this research paper we have briefly discussed about Euclidean vector. They have recommended guaranteeing the full diversity is significant. They have proposed the need of streamlining of the pivot to get the specific likelihood of blunder. The item measures depend on the likelihood of mistake. They have given a logical view to the ideal turn points.
It is talked about based on the Euclidean space. Their point is to get the most brief Euclidean distance. Their methodology depends on different point bases and triangular obstacles based. First the turning centers around the courses are portrayed as the irrelevant spotlights on the deviation lines from guide sources toward obstacles raised. By then, search the raster cells according to specific principles of characterizing Review Article Abstract Euclidean space is the calculative technique for the computation of the inward and external places.
The arrangement of focuses for the computation is known as the Euclidean space. It is likewise utilized as Euclidean distance. It is utilized in various spaces and in their applications. It’s commonly used for bunching and characterization calculations, as well as a wide range of materialness in measurements.
The Euclidean space and its helpful applications have been researched and discussed in this study in light of the possibilities of the aforesaid viewpoint. The main goal is to focus, and it includes the area of materiality as well as an examination of computational practicality by looking at previous work. Watchwords Computational investigation, Euclidean space, Distance focuses, Functional application Interconnect them to form paths that show the shortest detachments from sources to targets while avoiding obstructions, according to the Global Journal of Advanced Technology and Engineering Exploration.
The most important systems of this estimation are to determine whether a straight path is passing a deterrent, to characterize extremely significant events, and so on. This approach gives the uniqueness portrayals in a changed pseudo-Euclidean space. By then, the information of the distinction builds allocation of each and every order is achieved relies upon high-demand experiences of trios of neighbor centers for each image data. Finally, a biggest deduced computation with the information of Gaussian Mixture Model and triplet divergence builds scattering is embraced to assess the congruity of each and every grouping in the data set for every data new picture.
Test results on an extensively valuable picture data set show that reasonability and viability of the proposed MAPHOR plan. The premise of the conversation is the space missions. They have investigated the encoding calculation first. They have considered occurrence vector of focuses and lines for the parity check grid in Euclidean math. For the generator grid calculation, it is gotten from tackling lattice condition over GF. They have proposed another encoding circuit of utilizing criticism shift registers in view of the semi cyclic grid. They have planned last, sequential encoding circuit for asset advancement and equal encoding circuit for speed enhancement.
Their outcomes show that the encoding plan is effective for the space correspondences. It examined the issue of directing calculation on hexagonal organizations. They have made a diagonal direction framework for tending to the hexagonal hubs in light of Euclidean space. Then, at that point, they have created ideal steering calculations. It is created by utilizing the vectors and points of the reclassified Euclidean space. They have contrasted their methodology and the conventional 3-headings plot and the Cayley diagram strategy. Their outcomes demonstrate that their calculation is more proficient. It is additionally absolutely free.
They have additionally demonstrated that the way is short in all the total trial and error. They have recommended huge upward due to steering. Because of this upward the exhibition and the adaptability of the organization corrupts. They have recommended that the geographic directing conventions are profoundly versatile in light of the stateless steering.
They have examined the irregularity between the two geographies. As per the creators the exhibition of the organization increments on the off chance that the organizations are implanted in Hyperbolic Space as opposed to Euclidean Space. They have assessed the presentation of ravenous steering. The primary premise of examination is exaggerated space and Euclidean space. Their evaluation is based on their rate of progress and bounce stretch metrics. It has been considered in relation to the frameworks in charge of information transmissions. In Euclidean space, they have cultivated pseudo-irregular codes. Their model appears as parts of affirmation of pseudorandom structures with a limited reach, similar to conveyors of code words. It is used in the creation of fictitious brain organizations.
They’ve proposed a category of mental organizations. It is proposed with the property of broad estimation. The integrable capacities of Lebesgue have been used. The non-Euclidean vector item determines this. In comparison to similar methodologies, their findings justify the recommended strategy progress. The discussion is based on the polarization-specific gathering. They looked into the course finder and the calculation for determining direction. The four-component radio determines this.
The speculative assessment with proof of essential hypotheses, which are theoretical foundation of the bearing finding computation in conditions of weakness and short lived dubiousness of got signal polarization circles have been thought of. Their outcomes show that the increment of the sign space produces positive result. They have proposed that the comparing space designs of video portrayal are overlook in the past examination work. They have tended to the activity acknowledgment task with a spatial-transient portrayal examination calculation with Grassmannian complex and Euclidean space Transient elements have been separated from every video test. It has been finished with the direction following technique. It is examined in the setting by implanting them.
They have directed the Grassmannian complex and Euclidean space with the multi-piece. The outcomes support the methodology They have proposed that a large portion of the calculations diminish the conveyance disparity in the information spaces for this issue. They have proposed the factual properties are significant in the event of kernel based learning machine that is imitating portion Hilbert spaces. They have proposed an original procedure for matching disseminations. It is accomplished by covariance arrangement.
This technique is an in view of the Euclidean spaces to limitless layered highlight spaces. They have proposed an original system for matching dispersions in It is accomplished to covariance arrangement. This methodology is an in light of the Euclidean spaces to endless layered highlight spaces. They have given two arrangement draws near. By this they have accomplished shut structure articulations through part grids. Their outcomes show that their methodologies beat in both precision and productivity. The following are the figures of Euclidean space.
Problem domain
The following assertions have been distinguished in light of the conversation and assessment of previous exploratory works:
1) In a few sectors, there is a requirement for information mining to be linked to Euclidean space for improved example point disclosure.
2) There is a need to reduce autocorrelation.
3) In terms of data of interest and space disjoints, there is a need for blunder assessment.
4) When it comes to trait and boundary varieties, considerations of the area of bend, relapse, and coefficient vectors are required.
5) For the intricate issue, there is a requirement to increase the linkup with the Euclidean space.
Analysis
We have studied different writing connected with the Euclidean space with various application regions has been talked about and examined. The fundamental boundaries are technique and the outcomes assessment boundaries. The examination of the most recent techniques featured the effects have been talked about in Table 1.
| S.No. | Method | Computation approach |
| 1 | Space like translating solitons space. | In pseudo-Euclidean space, they examined the parametric and non-parametric versions of the rigidity theorem of spacelike translating solitons. |
| 2 | Hypersurfaces
in Euclidean Space |
They’ve given it a categorization. It’s a graph with a constant mean curvature that’s been generalized. Gauss-Kronecker curvature is another name for this. |
| 3 | Steiner minimal trees in Euclidean space | They discussed the topology of Steiner minimum trees and their attributes. They also looked at the use of Steiner points and their geometric position. |
| 4 | Complete curvature scale space
representation |
Local shape curve features have been proposed by them. Under planar Euclidean transformations, it is helpful and invariant. It is also unaffected by the parameterization of the curve. |
| 5 | MA-digitization of 2D Euclidean spaces | A homotropy has been provided. They gave the homotropy the name LMA-homotropy and investigated it using the LMA-homotropy equivalence for Euclidean and M-topologies. |
| 6 | Immersion in Euclidean spaces | In Euclidean space, they researched and debated compact immersed orientable hypersurfaces. They talked about the tangential and normal components to see if they were suitable. |
Conclusion and future suggestions
The review and discussion in this work were done using four-way angles. The paper has been distinguished from numerous domains related to Euclidean space in the most fundamental way. In the second manner the strategies have been indented for the conversation. In the third angles the boundaries and the qualities utilized have been talked about with the benefits and hindrances. At last, in light of the review arrangements and effect have been examined, dissected and profound penetrating calculation connect up has been measured for the mix.
The following are the categories for future work:
- The coding and encoding component can be used to break down and find the influence of the mix with different systems in correspondence.
- It tends to be consolidated in order to make computational calculations like grouping and order easier to employ.
- Future exploration work could be influenced by the relevance of combining these methodologies.
Related Topics:
- what are the row spaces, column spaces and null spaces in Linear Algebra?
- How to solve system of linear equations in Linear Algebra?
- what is the vector space in linear algebra? vector space example
- How to test the given vectors are linearly independent or not?
- What are the matrices and their types ?
- Finding Eigen Values and Eigen Vectors using MATLAB
- How to diagonalize a matrix? Example of diagonalization
- What are the shortcuts for finding the determinant of a matrix?
- What are the Block Matrices?
- what are the examples of scalar and vector quantities?
- How to perform similar matrices transformation?
- How to find the basis of a vector space V?
- what are the eigen values and eigen vectors? explain with examples
- What are the nodal incidence matrices?
- What is the span of a vector space?
- Study of Linear Transformation and its Application